【数模学习笔记】层次分析法（AHP）的原理和过程详解

2025-06-08 3 条评论

前言和简述

这个模型是用来解决什么问题的？

用来解决评价类问题。对于有多个评价指标的评价体系，来决定最佳的方案（通过确认权重）。

通过在不同的条件下，两两比较指标（矩阵的形式），最后综合起来，来确定最终的权重。（这些权重在人的一般思维过程中是定性的，而在层次分析法中要给出得到权重的定量方法）

为什么需要学习这个模型？它在数学建模中的地位或常用性如何？

在生活中应用这个模型的渠道是非常广的，特别是那些需要主观决策的、或者需要用经验判断的决策方案，例如：

买房子（主观决策）
选择旅游地（主观决策）
给员工进行绩效评估（经验判断）
选择开店地址（经验判断）

过程

整体思路如下图所示：

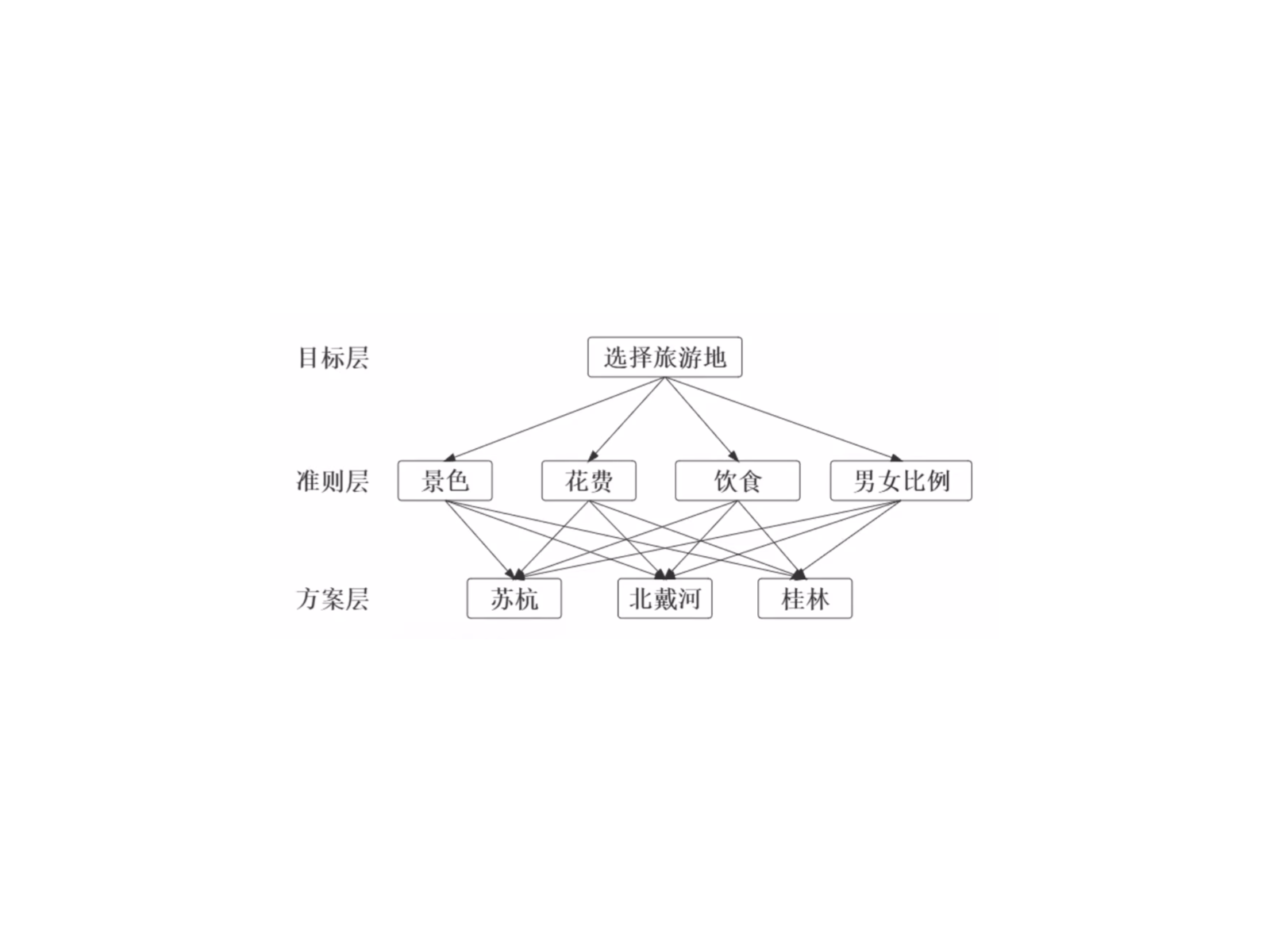
画出层级结构图（目标层、准则层、方案层）（图需要出现在论文里）

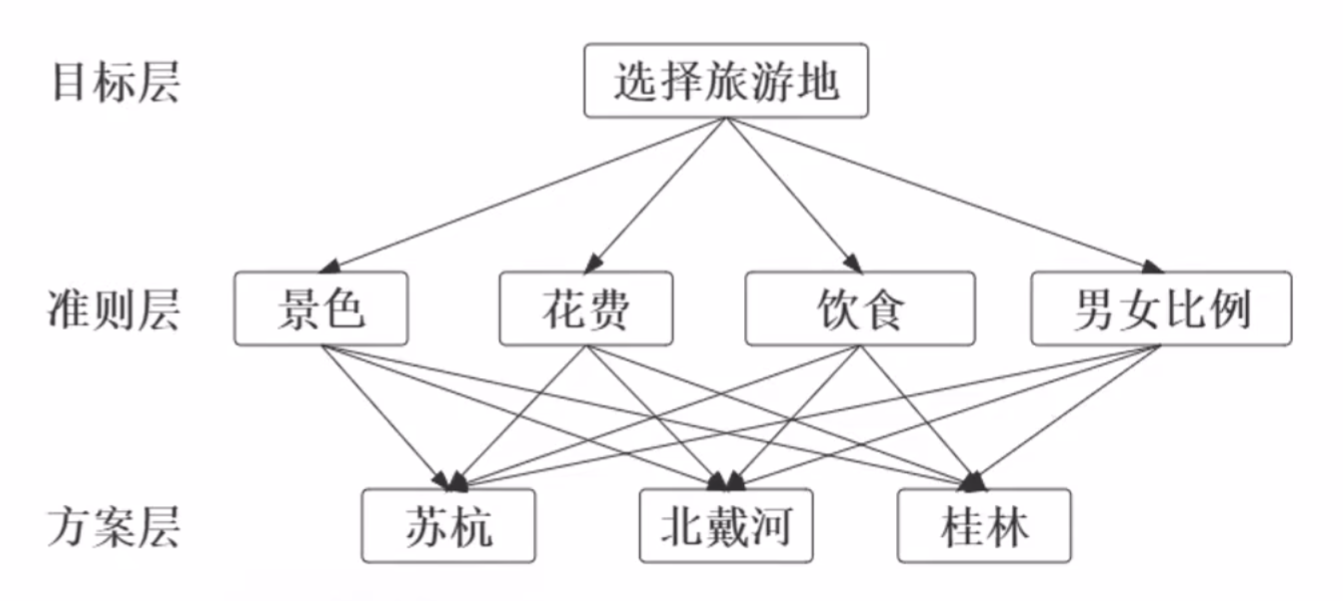
层级结构图 类似上面这张图，有三层（目标层、准则层、方案层）。

准则层 指我们设定的不同的指标，后续需要算出具体的权重。准则层可以有很多层，如果不止一层，就要像下图这样添加。

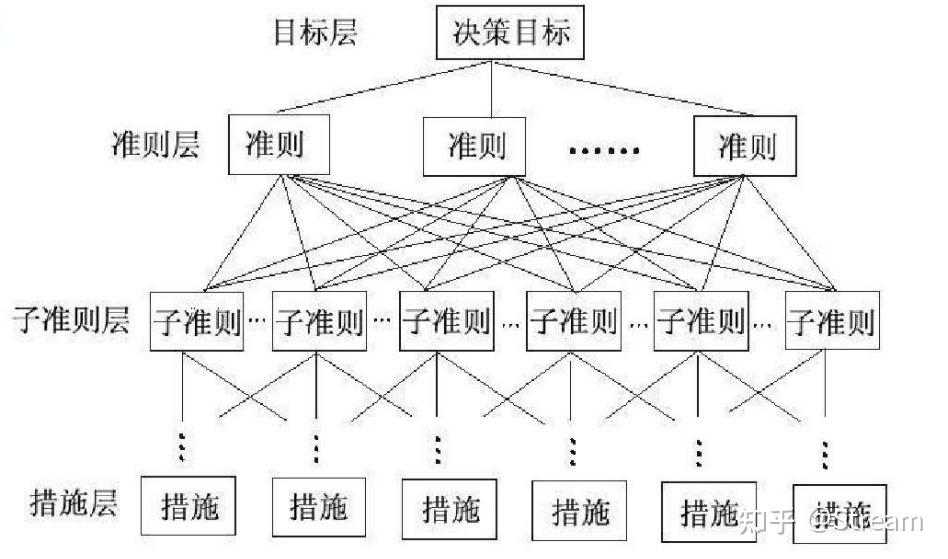
image-20250605155810143
方案层 指我们最终的方案选项

构造判断矩阵（确定评价指标的孰重孰轻。也就是不同指标的权重）

一共大抵有两步，第一步是要先确定指准则的重要性（层次单排序），第二步是要确定不同方案在某一准则下的得分（层次总排序）。

对于我们要构建的任意一个矩阵，设 $A= (a_ {ij})_ {m\times n} $ ，需要满足以下条件：

$a_{ij}>0$
$a_{ij}=\frac{1}{a_{ji}}$
$a_{ii}=1$

依照评价指标对各个方案进行打分

有了矩阵之后我们就要往里面填充内容了。

第一步（层次单排序）：我们要将每两个准则之间两两对比（打分），看看哪个更重要、有多重要。判断的尺度如下：

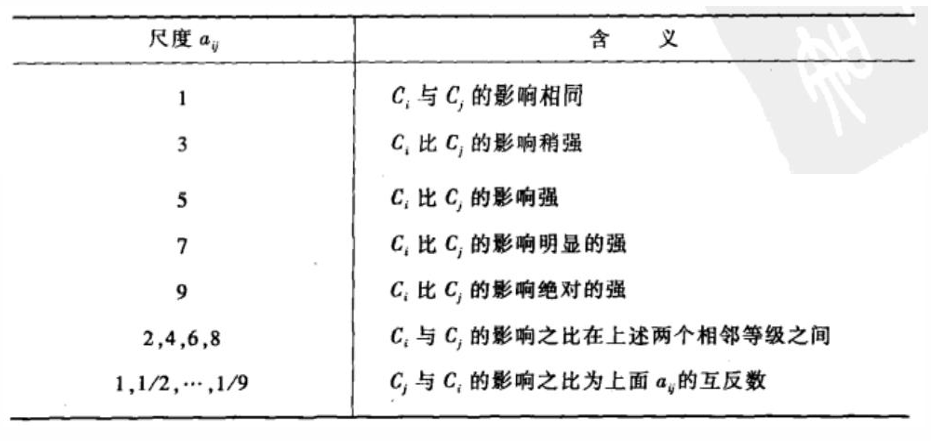
判断矩阵大概会变成下面这样（以此类推）：

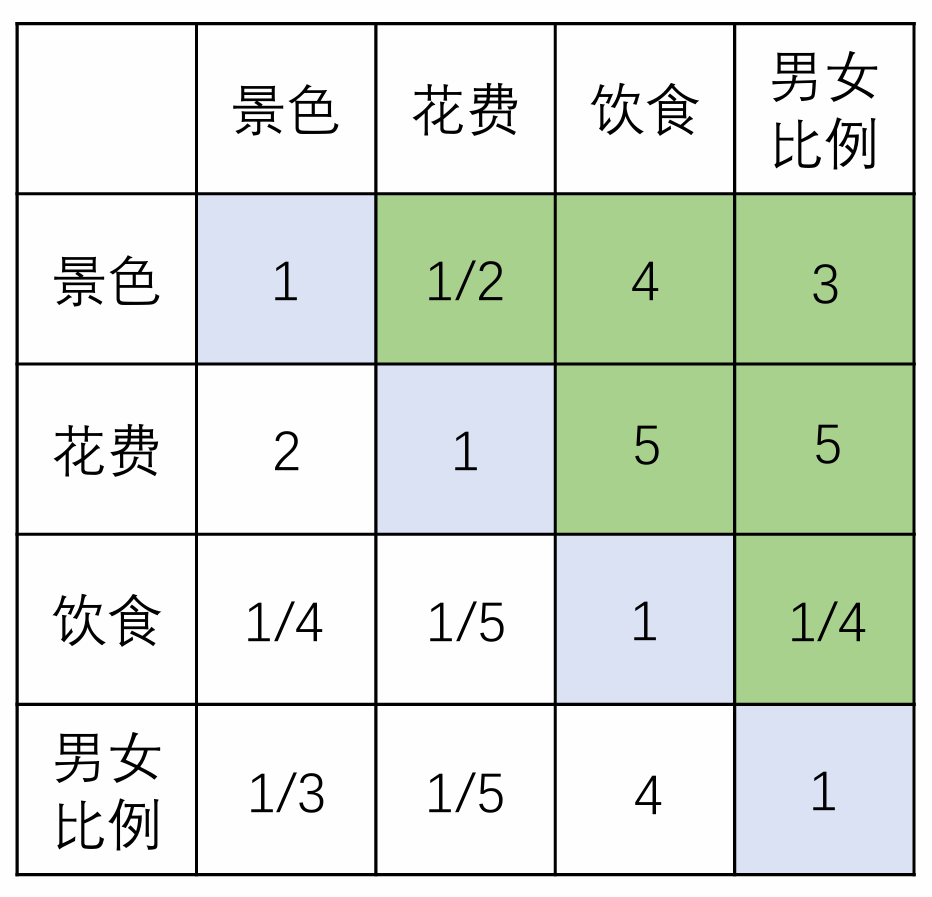
我们可以发现上面所说的三个条件的由来（简要解释）：

$a_{ij}>0$：因为要让整个矩阵的元素都 > 0，方便后续计算

$a_{ij}=\frac{1}{a_{ji}}$ ：因为一个重要，另一个就不重要，要平衡

$a_{ii}=1$：自己和自己比，当然是相同重要

第二步（层次总排序）：我们要在每个准则下，通过两两比较来打分，从而完善矩阵。矩阵的数量和准则的数量相同。（同样需要满足以上三个条件）

大概会变成下面这样：

求出权重（层次单排序）

上面的矩阵打分完成后，我们要计算它们的权重（权重向量）

计算权重有两种方法：算数平均法、特征值法（更常用）

算数平均法

首先，根据下面这个公式，得到每一行的 m 维向量

$$ \bar{w_{i}}=\sqrt [m]{\prod_{j = 1}^{m}{a_{ij}}} $$

计算完成后类似：

景色：

$\sqrt[4]{1 \times \frac{1}{2} \times 4 \times 3} = \sqrt[4]{6} \approx 1.5651$

花费：

$\sqrt[4]{2 \times 1 \times 5 \times 5} = \sqrt[4]{50} \approx 2.6593$

饮食：

$\sqrt[4]{\frac{1}{4} \times \frac{1}{5} \times 1 \times \frac{1}{4}} = \sqrt[4]{\frac{1}{320}} \approx 0.3162$

男女比例：

$\sqrt[4]{\frac{1}{3} \times \frac{1}{5} \times 4 \times 1} = \sqrt[4]{\frac{4}{15}} \approx 0.6813$

上述是未归一化（也叫标准化）的权重向量。我们需要进一步归一化。可以根据下面这个公式，将每一项除以总和，即：

$$ w_i = \frac{\bar{w_i}}{\sum_{j = 1}^{m} \bar{w_j}} $$

计算完成后类似：

总和：$1.5651 + 2.6593 + 0.3162 + 0.6813 = 5.2219$

景色：$\frac{1.5651}{5.2219} \approx 0.2996$

花费：$\frac{2.6593}{5.2219} \approx 0.5092$

饮食：$\frac{0.3162}{5.2219} \approx 0.0605$

男女比例：$\frac{0.6813}{5.2219} \approx 0.1305$

最终通过算数平均法得到的权重向量 W 为：

$$ W = \begin{pmatrix} 0.2996 \\ 0.5092 \\ 0.0605 \\ 0.1305 \end{pmatrix} $$

特征值法

除了算数平均法，特征值法是另一种计算权重向量的方法。这种方法在AHP理论中占据核心地位。在实际比赛和科研中，用特征值法求权重更常用也更方便。在非一致性不大的情况下，二者算出的权重相差也并不大，可实际生活中的数据一致性并非那么强，因此建议用特征值法。当然为了凑字数的话也可以两种方法都用，然后取其平均值。

特征值法的核心思想是，对于一个判断矩阵 $A$，我们希望找到一个权重向量 $w$，使得 $A$ 乘以 $w$ 的结果约等于 $w$ 本身乘以一个常数（这个常数就是最大特征值 $\lambda_{max}$）。数学上表示为：

$$ Aw = \lambda_{max}w $$ 这里的 $w$ 就是对应于最大特征值 $\lambda_{max}$ 的特征向量。我们通过求解这个特征向量，并将其归一化，就可以得到各个指标的权重。

步骤如下：

构造判断矩阵 $A$ 我们继续使用2.3的判断矩阵 $A$： $$ E= \left( \begin{matrix} 1 & 1/2 & 4 & 3 \ 2 & 1 & 5 & 5 \ 1/4 & 1/5 & 1 & 1/4 \ 1/3 & 1/5 & 4 & 1 \ \end{matrix} \right) $$
计算矩阵 $A$ 的最大特征值 $\lambda_{max}$ 及其对应的特征向量 $\alpha$

直接用数学软件（ MATLAB、Python的NumPy库等）来计算。

软件会计算出矩阵 $E$ 的所有特征值，我们选取其中最大的那个实数特征值，即为 $\lambda_{max}$。同时，软件也会给出与 $\lambda_{max}$ 相对应的特征向量 $\alpha$。

计算得到：
- 最大特征值 $\lambda_{max} \approx 4.2201$
- 对应的特征向量 $\alpha$： $$ \alpha \approx \begin{pmatrix} -0.5568 \ -0.7925 \ -0.1085 \ -0.2319 \end{pmatrix} $$
  
  注意：这里的负号仅仅是计算过程中得到的一种表示，特征向量乘以任意非零常数后仍是特征向量，这里重要的是各分量之间的比例关系。
对特征向量 $\alpha$ 进行归一化处理，得到权重向量 $w$

归一化的公式如下： $$ w_i = \frac{|\alpha_i|}{\sum_{j=1}^{n} |\alpha_j|} $$ 其中 $n$ 是矩阵的阶数（这里 $n=4$）。

$\alpha \approx (-0.5568, -0.7925, -0.1085, -0.2319)^T$:

分母：$S = |-0.5568| + |-0.7925| + |-0.1085| + |-0.2319| = 1.6897$

然后除以总和 $S$： $w_{\text{景色}} = \frac{|-0.5568|}{1.6897} \approx 0.3295$ $w_{\text{花费}} = \frac{|-0.7925|}{1.6897} \approx 0.4690$ $w_{\text{饮食}} = \frac{|-0.1085|}{1.6897} \approx 0.0642$ $w_{\text{男女比例}} = \frac{|-0.2319|}{1.6897} \approx 0.1373$

最终通过特征值法得到的权重向量 $W$ 为： $$ W = \begin{pmatrix} 0.3295 \\ 0.4690 \\ 0.0642 \\ 0.1373 \end{pmatrix} $$

根据下表的比较，我们可以看到，这个结果与之前用算术平均法得到的结果略有差异。这很正常，因为它们是两种不同的计算（或近似）方法。

算术平均法特征值法

景色 0.2996 0.3295

花费 0.5092 0.4690

饮食 0.0605 0.0642

男女比例 0.1305 0.1373

	算术平均法	特征值法
景色	0.2996	0.3295
花费	0.5092	0.4690
饮食	0.0605	0.0642
男女比例	0.1305	0.1373

一致性检验（层次单排序）

在判断其一致性是否通过之前，我们需要先计算$CI$、$RI$值，再求解$CR$值，根据他们来判断。

在上一步我们求出权重矩阵之后。要求出 CI，得先求出 $\lambda{max}$，计算公式如下：

$$ \lambda{max}=\frac{1}{n}\sum_{i = 1}^{n}\frac{(AW)_{i}}{w_{i}} $$ 其中 $n$ 为维度的数量（例如构建的判断矩阵中的：景色、花费、饮食、男女比例时，$n=4$）；$A$为我们刚刚构建的判断矩阵；$W$为我们构建的判断矩阵；$(AW)_i$为矩阵$A$和向量$W$相乘（叉乘）后，得到的新向量的第$i$个元素。

比如判断矩阵 $A$ 为：

$$ E= \left( \begin{matrix} 1 & 1/2 & 4 & 3 \\ 2 & 1 & 5 & 5 \\ 1/4 & 1/5 & 1 & 1/4 \\ 1/3 & 1/5 & 4 & 1 \\ \end{matrix} \right) $$ 归一化后的权重 $W$（即我们刚刚计算出来的权重向量，这里用算数平均法得出的结果举例）为

景色	花费	饮食	男女比例
0.2996	0.5092	0.0605	0.1305

$$ W= \left( \begin{matrix} 0.2996\\ 0.5092\\ 0.0605\\ 0.1305\\ \end{matrix} \right) $$

我们可以计算$AW$：

$$ AW = \left( \begin{matrix} 1 & 1/2 & 4 & 3 \\ 2 & 1 & 5 & 5 \\ 1/4 & 1/5 & 1 & 1/4 \\ 1/3 & 1/5 & 4 & 1 \\ \end{matrix} \right) \times \left( \begin{matrix} 0.2996 \\ 0.5092 \\ 0.0605 \\ 0.1305 \\ \end{matrix} \right) = \left( \begin{matrix} 1.1877 \\ 2.0634 \\ 0.2699 \\ 0.5742 \\ \end{matrix} \right) $$

	景色	花费	饮食	男女比例	权重值	$AW$
景色	0.2996	0.2546	0.2420	0.3915	0.2996	1.1877
花费	0.5992	0.5092	0.3025	0.6525	0.5092	2.0634
饮食	0.0749	0.1018	0.0605	0.0326	0.0605	0.2698
男女比例	0.0999	0.1018	0.2420	0.1305	0.2420	0.5742

求出$AW$之后就可以计算$\lambda_{max}$：

$$ \lambda{max}=\frac{1}{n}\sum_{i = 1}^{n}\frac{(AW)_{i}}{w_{i}} \\ =\frac{1}{4} \left( \frac{1.1877}{0.2996} + \frac{2.0634}{0.5092} + \frac{0.2699}{0.0605} + \frac{0.5742}{0.1305} \right) \\ =4.2201 $$

求出$\lambda_{maax}$之后，$CI$值就好算多了，我们可以根据新下面的公式来计算：

$$ CI=\frac{\lambda_{max}-n}{n-1} \\ $$ 代入我们刚刚计算出来的$\lambda_{max}$： $$ CI=\frac{4.2201-4}{4-1}=0.0734 $$ 关于$RI$的值，我们可以通过查表得到： $$ \begin{array}{c|ccccccccccccccc} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 \\ \hline RI & 0.00 & 0.00 & 0.58 & 0.90 & 1.12 & 1.24 & 1.32 & 1.41 & 1.45 & 1.49 & 1.51 & 1.48 & 1.56 & 1.57 & 1.59 \end{array} $$ 有了$CI$和$RI$后，我们就可以算出$CR$： $$ CR=\frac{CR}{RI} $$ 由于我们的矩阵是4阶，所以$RI$为$0.90$。接下来将我们上面得到的$CI$和$RI$代入： $$ CR=\frac{0.0734}{0.90}=0.0816 $$ 太好了！我们的$CR$值小于0.1，意思就是我们这个矩阵是一致矩阵，一致性检验就这样通过啦！

什么是矩阵一致性？

这是在线性代数中的一个重要概念，主要用来描述线性方程组是否有解。

定义：

一个线性方程组 ($A\mathbf{x} = \mathbf{b} $) 是一致的（有解），当且仅当满足以下条件： $$ \text{rank}(A) = \text{rank}([A|\mathbf{b}]) $$

其中：

$A$是方程组的系数矩阵（$m \times n $），

( $[A|\mathbf{b}] $) 是增广矩阵（在$A$右侧添加常数列$\mathbf{b}$)，

$\text{rank}$表示矩阵的秩（即矩阵中线性无关的行或列向量的最大数目）。

对于一致矩阵，具有两个性质：

$A$的秩1，$A$的唯一非零特征根为$n$；

$A$的任一列向量都是对于特征根$n$的特征向量

从性质1也可以说，只要满足两两行/列成倍数关系，就是一致性矩阵。

通过进行一致性检验，我们可以认为判断矩阵是否具有可接受的一致性，是否符合传递性的逻辑（比如，如果认为 A>>B，B>>C，那么根据传递性，结论应是 A>>C）。

如何利用矩阵一致性发现错误？

用来检查判断矩阵“矛盾”的问题，所以在使用判断矩阵之前一定要先检验其一致性.

对于$CR$，$0.1$是个坎，小于0.1说明矩阵的一致性程度被认为在容许的范围内；如果大于等于0.1，说明我们在构建判断矩阵时出现了逻辑错误。

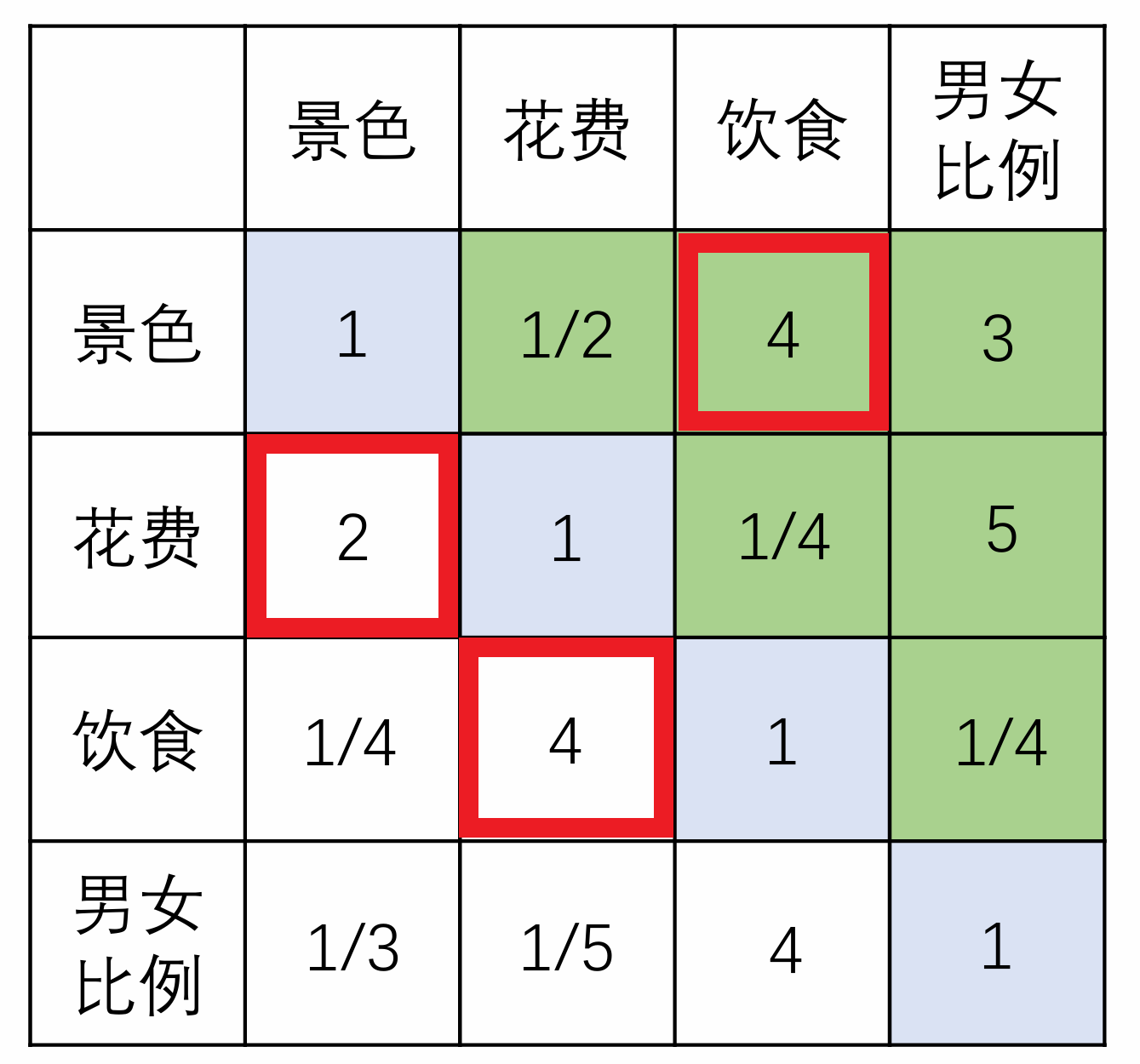
比如我们看下面这个矩阵，它的$CR$值可以算出是0.9882，远远超过了0.1，所以它是不一致矩阵。

image-20250607204823846

为啥它是不一致矩阵呢？我们发现，景色被认为比饮食重要（值为4），饮食又被认为比花费重要（值为4）。

按理来说，景色应远比花费重要（理论上接近 4×4=16 倍）。

然而，矩阵中花费却被认为比景色更重要 (值为2)，这肯定有问题，从而导致了极高的 CR 值。

找到问题之后，检查一下是不是不小心输错了，如果没输错，我们就要对矩阵进行修正。不能只是让数字变“好看”，要符合真实的偏好。我们可以针对矛盾点来思考（不需要修改所有数字，一般只需要修正那个最矛盾的判断点）：

A: “景色比饮食重要 (4)。”

B: “饮食比花费重要 (4)。”

C: “花费比景色重要 (2)。”

上面三句话不可能同时成立，必须要修改其中一个。可能你想了想觉得“花费比景色重要”这个判断最靠谱。那么你就必须承认，景色 vs 饮食 或 饮食 vs 花费 的判断太过夸张了。也许饮食只是比花费“稍微重要”一点（比如从4改成2），而不是重要得多。

修改的过程中，不要忘记要同步修改它的倒数。

修改完成后，我们需要重新计算矩阵的$CR$值，如果仍然大于等于0.1，说明还是有问题，需要继续修改。不断调整知道矩阵的$CR$值小于0.1，即通过一致性检验。

求出权重（层次总排序）

刚刚我们根据不同的准则计算出了权重。接下来我们要用几乎相同的方法，计算在每个准则下，不同方案的权重。

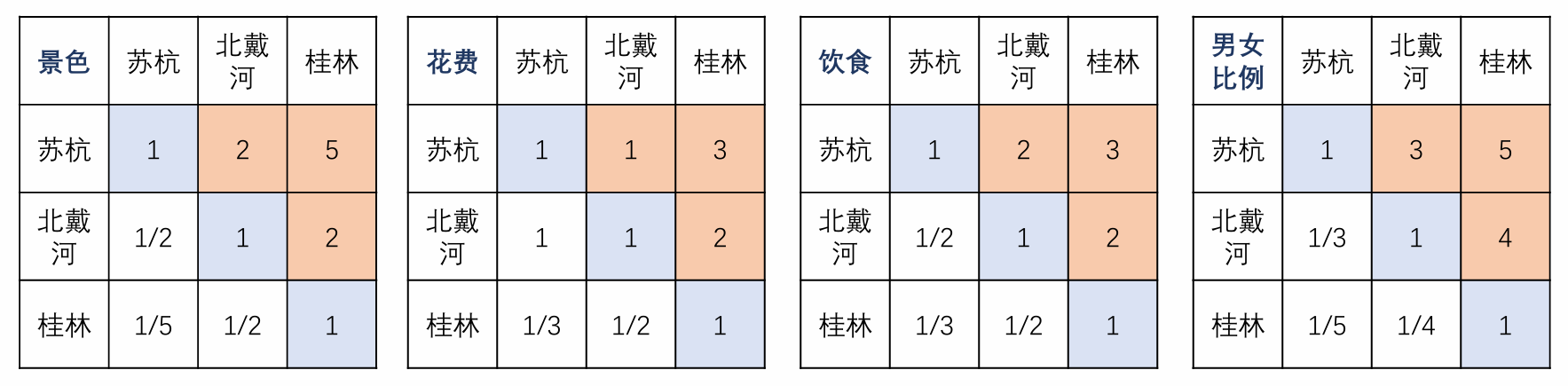
这些是我们在2.3的时候打的分：

算数平均法

与“层次单排序”中介绍的算数平均法（2.4.1）几乎完全相同。我们以景色准则下的方案比较矩阵为例：

景色	苏杭	北戴河	桂林
苏杭	1	2	5
北戴河	1/2	1	2
桂林	1/5	1/2	1

计算各方案的$\bar{w_i}$ (这里 $m=3$，因为有3个方案)：
- 苏杭：$\bar{w}_{\text{苏杭}} = \sqrt[3]{1 \times 2 \times 5} = \sqrt[3]{10} \approx 2.1544$
- 北戴河：$\bar{w}_{\text{北戴河}} = \sqrt[3]{1/2 \times 1 \times 2} = \sqrt[3]{1} = 1.0000$
- 桂林：$\bar{w}_{\text{桂林}} = \sqrt[3]{1/5 \times 1/2 \times 1} = \sqrt[3]{1/10} \approx 0.4642$
归一化得到权重向量 $W_{\text{景色}}$：
- 总和 $\sum \bar{w_j} = 2.1544 + 1.0000 + 0.4642 = 3.6186$
- $W_{\text{景色}}(\text{苏杭}) = \frac{2.1544}{3.6186} \approx 0.5954$
- $W_{\text{景色}}(\text{北戴河}) = \frac{1.0000}{3.6186} \approx 0.2764$
- $W_{\text{景色}}(\text{桂林}) = \frac{0.4642}{3.6186} \approx 0.1283$

对其他准则（花费、饮食、男女比例）下的方案比较矩阵也进行同样的操作，我们可以得到它们各自的权重向量：

$W_{\text{花费}}$：
- 苏杭: $\approx 0.4434$
- 北戴河: $\approx 0.3874$
- 桂林: $\approx 0.1692$
$W_{\text{饮食}}$：
- 苏杭: $\approx 0.5396$
- 北戴河: $\approx 0.2969$
- 桂林: $\approx 0.1634$
$W_{\text{男女比例}}$：
- 苏杭: $\approx 0.6267$
- 北戴河: $\approx 0.2797$
- 桂林: $\approx 0.0936$

这些权重向量分别表示在单一准则下，各个方案的优劣排序。

特征值法

与层次单排序中计算准则权重（2.4.2）几乎完全相同，特征值法也是计算方案层权重更常用和理论上更优的方法。对于每个准则下的方案比较矩阵，我们都进行如下操作：

构造对应准则下的方案判断矩阵 $A_k$ (例如 $A_{\text{景色}}$)。以上述“景色”准则的判断矩阵为例： $$ A_{\text{景色}} = \begin{pmatrix} 1 & 2 & 5 \ 1/2 & 1 & 2 \ 1/5 & 1/2 & 1 \end{pmatrix} $$
计算矩阵 $A_k$ 的最大特征值 $\lambda_{max}^{(k)}$ 及其对应的特征向量 $\alpha^{(k)}$。使用数学软件（如 MATLAB, Python NumPy）计算。对于 $A_{\text{景色}}$：
- 最大特征值 $\lambda_{max}^{\text{(景色)}} \approx 3.0385$
- 对应的特征向量 $\alpha^{\text{(景色)}} \approx \begin{pmatrix} 0.8351 \ 0.4569 \ 0.2976 \end{pmatrix}$
对特征向量 $\alpha^{(k)}$ 进行归一化处理，得到该准则下的权重向量 $W_k$。 $W_{\text{景色 (特征值)}} (\text{苏杭}) = \frac{0.8351}{0.8351 + 0.4569 + 0.2976} = \frac{0.8351}{1.5896} \approx 0.5254$ $W_{\text{景色 (特征值)}} (\text{北戴河}) = \frac{0.4569}{1.5896} \approx 0.2874$ $W_{\text{景色 (特征值)}} (\text{桂林}) = \frac{0.2976}{1.5896} \approx 0.1872$

所以，在“景色”准则下，通过特征值法得到的方案权重向量为： $W_{\text{景色 (特征值)}} = (0.5254, 0.2874, 0.1872)^T$

可以看到，这个结果与算术平均法得到的结果 ($0.5954, 0.2764, 0.1283)^T$ 略有不同，这是正常的，因为它们是基于不同原理的计算方法。

同样地，对其他准则（花费、饮食、男女比例）的方案比较判断矩阵，也分别应用特征值法计算其权重向量：

$W_{\text{花费 (特征值)}} \approx (0.4300, 0.3950, 0.1750)^T$
$W_{\text{饮食 (特征值)}} \approx (0.5500, 0.2900, 0.1600)^T$
$W_{\text{男女比例 (特征值)}} \approx (0.6150, 0.2850, 0.1000)^T$

完成这些计算后，我们得到了在每个准则下各个方案的相对权重。下一步就是进行一致性检验。

一致性检验（层次总排序）

与“层次单排序”中的准则比较矩阵一样，这里的每一个方案的矩阵也必须进行一致性检验。这是为了确保我们在对各个准则下的方案进行两两比较时，逻辑上没有出现大的矛盾。

检验的步骤和公式与之前完全相同：

计算最大特征根 $\lambda_{max} = \frac{1}{n}\sum_{i=1}^{n}\frac{(AW)_i}{w_i}$
计算一致性指标 $CI = \frac{\lambda_{max}-n}{n-1}$
计算一致性比例 $CR = \frac{CI}{RI}$

需要注意，这里的 $n$ 是方案的数量。在我们的例子中，方案是苏杭、北戴河、桂林，所以 $n=3$，所以查表可得$RI = 0.58$。

我们对每个方案的判断矩阵（景色、花费、饮食、男女比例这4个）都进行一致性检验。比如，对于上面计算过的“景色”矩阵（这里用2.6.1的算数平均法得出的结果举例）：计算得 $\lambda_{max} \approx 3.00553$。则 $CI = \frac{3.00553 - 3}{3-1} = \frac{0.00553}{2} \approx 0.002765$。于是 $CR = \frac{0.002765}{0.58} \approx 0.004767$。

因为 $0.004767 < 0.1$，所以“景色”这个准则下的方案比较矩阵的一致性检验通过啦。

每一个方案比较矩阵同样都必须通过一致性检验。如果有任何一个矩阵的 $CR \ge 0.1$，则说明在该准则下对方案的判断有逻辑矛盾，需要调整打分，直到通过一致性检验。

假设我们所有的方案比较矩阵都通过了一致性检验，那么我们就得到了：

准则层相对于目标层的权重向量 (来自层次单排序)。
方案层相对于每个准则的权重向量 (来自层次总排序)。

接下来，我们就可以将这些权重进行组合，计算出每个方案最终的总得分，从而选出最优方案了。

得出最佳的方案

经过前面一系列的打分、计算权重和一致性检验，我们现在手上有了两套关键的权重数据：

准则层的权重：表示我们认为各个评价指标（如景色、花费、饮食、男女比例）相对目标（选择最佳旅游地）的重要性。（在 2.4.2 特征值法 中，我们计算得到：$W_{\text{准则}} = (0.3295_{\text{景色}}, 0.4690_{\text{花费}}, 0.0642_{\text{饮食}}, 0.1373_{\text{男女比例}})^T$）

方案层在各准则下的权重：表示在每一个特定准则下，各个方案（苏杭、北戴河、桂林）的相对优劣。（在 2.6.2 特征值法 中，我们计算得到各方案在各准则下的权重向量，如下表：

准则 (权重)	苏杭	北戴河	桂林
景色 (0.3295)	0.5254	0.2874	0.1872
花费 (0.4690)	0.4300	0.3950	0.1750
饮食 (0.0642)	0.5500	0.2900	0.1600
男女比例 (0.1373)	0.6150	0.2850	0.1000

现在，我们要做的就是将这两套权重“组合”起来，计算出每个方案的最终总得分，公式如下：

$$ \text{方案}_i \text{ 总得分} = \sum_{j=1}^{k} (W_{\text{准则}_j} \times W_{\text{方案}_i \text{ 在准则}_j \text{下}}) $$ 其中，$k$ 是准则的个数。

各个旅游地的最终总得分：

1. 苏杭：

$$ \begin{aligned} \text{得分}_{\text{苏杭}} &= (W_{\text{景色}} \times W_{\text{苏杭在景色下}}) + (W_{\text{花费}} \times W_{\text{苏杭在花费下}}) \\ & \quad + (W_{\text{饮食}} \times W_{\text{苏杭在饮食下}}) + (W_{\text{男女比例}} \times W_{\text{苏杭在男女比例下}}) \\ &= (0.3295 \times 0.5254) + (0.4690 \times 0.4300) \\ & \quad + (0.0642 \times 0.5500) + (0.1373 \times 0.6150) \\ &= 0.1731173 + 0.20167 + 0.03531 + 0.0844395 \\ &\approx 0.4945 \end{aligned} $$

2. 北戴河：

$$ \begin{aligned} \text{得分}_{\text{北戴河}} &= (0.3295 \times 0.2874) + (0.4690 \times 0.3950) \\ & \quad + (0.0642 \times 0.2900) + (0.1373 \times 0.2850) \\ &= 0.0947083 + 0.185255 + 0.018618 + 0.0391305 \\ &\approx 0.3377 \end{aligned} $$

3. 桂林：

$$ \begin{aligned} \text{得分}_{\text{桂林}} &= (0.3295 \times 0.1872) + (0.4690 \times 0.1750) \\ & \quad + (0.0642 \times 0.1600) + (0.1373 \times 0.1000) \\ &= 0.0616824 + 0.082075 + 0.010272 + 0.01373 \\ &\approx 0.1678 \end{aligned} $$

我们可以将计算过程和结果汇总成一个表格：

	景色	花费	饮食	男女比例	总得分	排名
苏杭	0.1731	0.2017	0.0353	0.0844	0.4945	1
北戴河	0.0947	0.1853	0.0186	0.0391	0.3377	2
桂林	0.0617	0.0821	0.0103	0.0137	0.1678	3
合计					1.0000

从最终的总得分来看：

苏杭：0.4945
北戴河：0.3377
桂林：0.1678

综上，苏杭是最佳的旅游目的地选择！

至此，我们通过层次分析法，将一个复杂的多标准决策问题，一步步量化，并得出了清晰的决策结果。

模型的优缺点:

优点

系统性和结构化：AHP将复杂问题分解为目标、准则、方案等多个层次。
处理定性与定量信息：定性 -> 定量。
简单直观，易于理解和操作：两两比较的方式符合人类的思维习惯，1-9的打分也容易掌握。不用数学背景也可以打分。
适用性广泛：AHP可以应用于各种领域的决策问题，如方案选择、资源分配、绩效评估、风险分析等，只要问题可以被层次化并且有多个评价标准。
提供量化结果和排序：最终能够给出各个方案的量化得分和排序，为决策提供了明确的依据。
包含一致性检验：一致性检验这个工具可以帮助判断是否存在逻辑矛盾。如果发现不一致，可以重新调整我们的判断。

缺点

主观性较强（对应第3个优点）：判断矩阵的构建依赖主观经验，如果分打的不好，结果会收到影响。garbage in, garbage out。
指标过多时工作量大（对应第2个优点）：当评价指标或方案数量较多时，需要进行的俩俩比较次数会急剧增加（$n(n-1)/2$次比较），导致耗时+判断疲劳。
一致性难以完全保证（对应第6个优点）：指标较多时，要使所有判断矩阵都通过一致性检验，并且保持判断的真实性，是很难的，可能要调很久。
指标间相互独立的假设：标准的AHP假设同一层次的指标之间是相互独立的。但实际上，指标间可能存在相互影响，AHP对此处理能力有限（需要更高级的网络层次分析法ANP等）。

我的思考与总结:

学习完层次分析法（AHP），我感觉像是打开了一扇新的窗户，原来那些看起来很主观、很“感觉化”的决策，也可以用这么有条理的数学方法来辅助。

新的理解：

学到了结构化思考、定性到定量、一致性的重要性。

难点与克服：

判断矩阵的填写：刚开始面对一堆指标，很容易比着比着就乱了。我是通过多看例子，尝试代入自己熟悉的情境来练习，慢慢找到感觉的。大师兄视频里的例子也很有帮助，跟着他的思路走一遍，理解会深刻很多。
特征值和特征向量的计算：这部分数学知识对我来说一开始是黑箱。虽然知道要用软件算，但还是想理解它背后的意义。后来明白，特征值法是为了找到一个最能代表判断矩阵传递关系的权重向量。目前阶段，我先学会怎么用软件得到结果，并理解结果的含义，数学原理等以后有机会再深入。
一致性调整：CR值超标时，调整判断矩阵很头疼。一开始可能会为了达标而随意修改，但后来意识到这违背了AHP的初衷。关键还是要回到最初的判断，思考哪个比较是最“不确定”或者最“矛盾”的，从那里入手，小幅调整，还有时刻保持自己的真实感受。

与其他模型的联系或区别（初步想法）：

AHP属于**多标准决策分析（MCDM）**方法的一种。它和其他一些评价类模型（比如后面会学到的TOPSIS法、模糊综合评价法等）都是为了解决“在多个标准下如何选优”的问题。
与一些纯粹基于客观数据的模型（比如线性规划、回归分析）不同，AHP非常依赖主观输入，这使得它能处理那些难以完全用客观数据衡量的决策，但也引入了主观性的风险。

注意事项：

明确目标和准则：在开始构建层次结构前，一定要花足够的时间思考最终的目标是什么，以及评价这个目标的准则有哪些。准则的选择对最终结果影响很大。也节约后续一致性调整的时间。
专家打分与集体决策：如果条件允许，可以让多位相关人员独立打分，然后综合他们的判断（比如对判断矩阵取几何平均），这样可以减少个人偏见。大师兄的视频里还提到说可以去知网找相关文献，看看他们的指标怎么打分的，我们可以借鉴。
软件辅助：计算权重和一致性检验时，一定要利用好MATLAB、Python，手算太麻烦也容易出错。
理解局限性：不要神化任何一个模型。在实际应用中，要根据实际情况调整。