博主头像
麟悟

好玩爱玩

作者头像 KylinOIO
头图

【数模学习笔记】整数规划（IP）的原理和过程详解

暂无评论

前言和简述

这个模型是用来解决什么问题的？

合适解决决策变量（部分或全部）必须取整数时的优化问题，不适合用LP。

主要处理：选择/决策类问题、分配/指派类问题、计数/数量类问题。

在供应链管理、生产调度、金融投资组合、物流网络设计等领域应用很多。

为什么需要学习这个模型？它在数学建模中的地位或常用性如何？

出场频率高、应用范围广。

许多竞赛题目背景本身就包含大量的离散决策。解决这类问题的基础，是能够准确识别并构建IP模型。

虽然整数规划问题属于NP-hard难题，理论求解难度随问题规模指数级增长，但现代优化求解器已经很强了，基本都能在可接受的时间捏计算出来。

核心原理

关于LP的原理讲解可以阅读[数模学习笔记】线性规划（LP）的原理和过程详解

IP与LP的核心区别在于变量的取值范围。LP的可行域是一个连续的凸多面体，其最优解必然在该多面体的某个顶点上达到。而IP的可行域是散落在多面体内部或边界上的一系列离散的整点。

千万别把把LP的最优解的自变量取整就是IP的最优解，这是错误的，原因：

  1. 四舍五入后的解可能不再满足原始的约束条件。
  2. 即使取整后的解是可行的，也大概率不是真正的整数最优解。

正因如此，IP才需要发展出专门求解算法（比如分支定界法）的原因。

在论文的引言或模型建立部分，可以阐述为何不能简单地对LP结果进行取整，比较严谨。

原理和计算步骤

计算过程图：

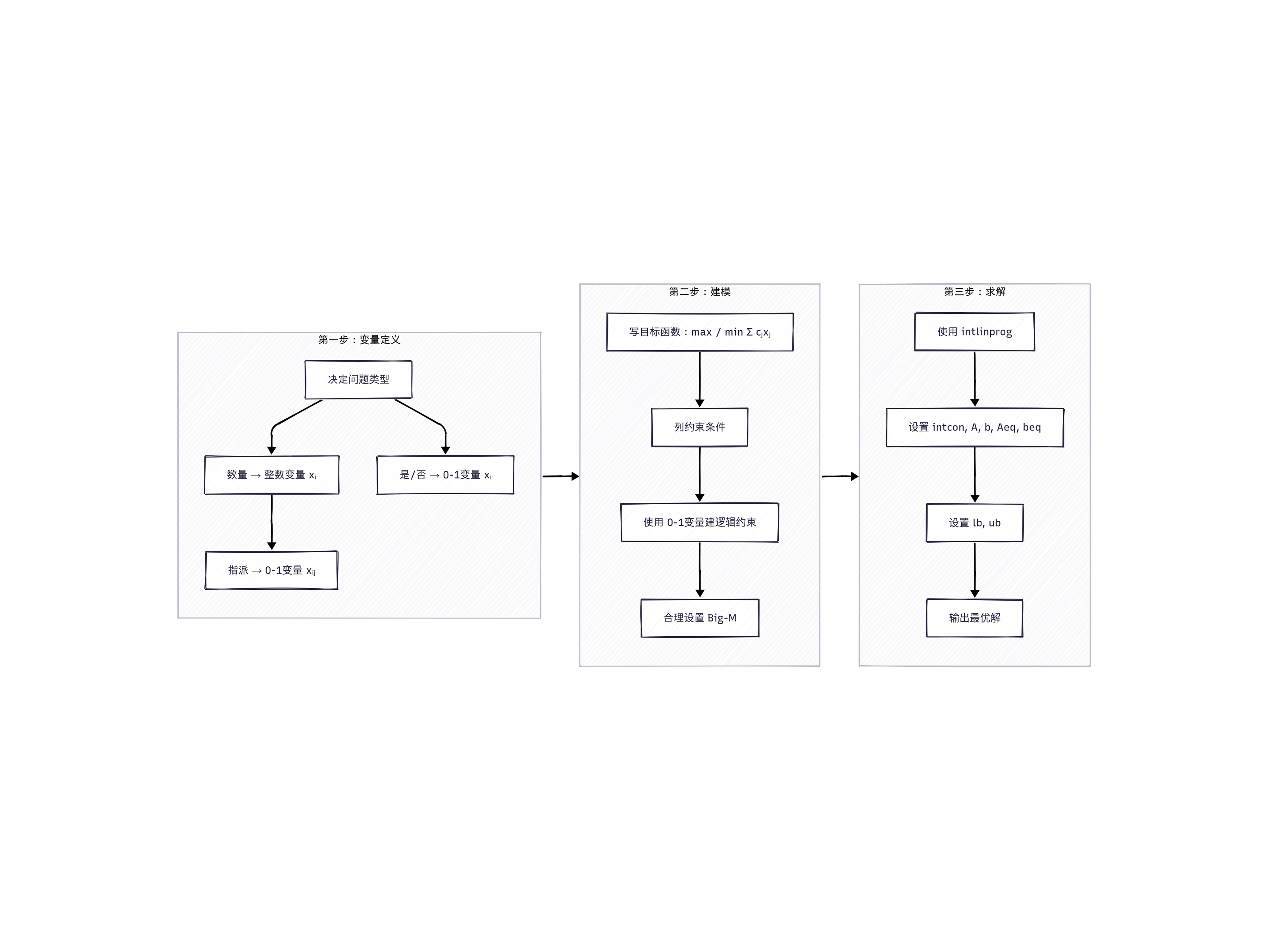
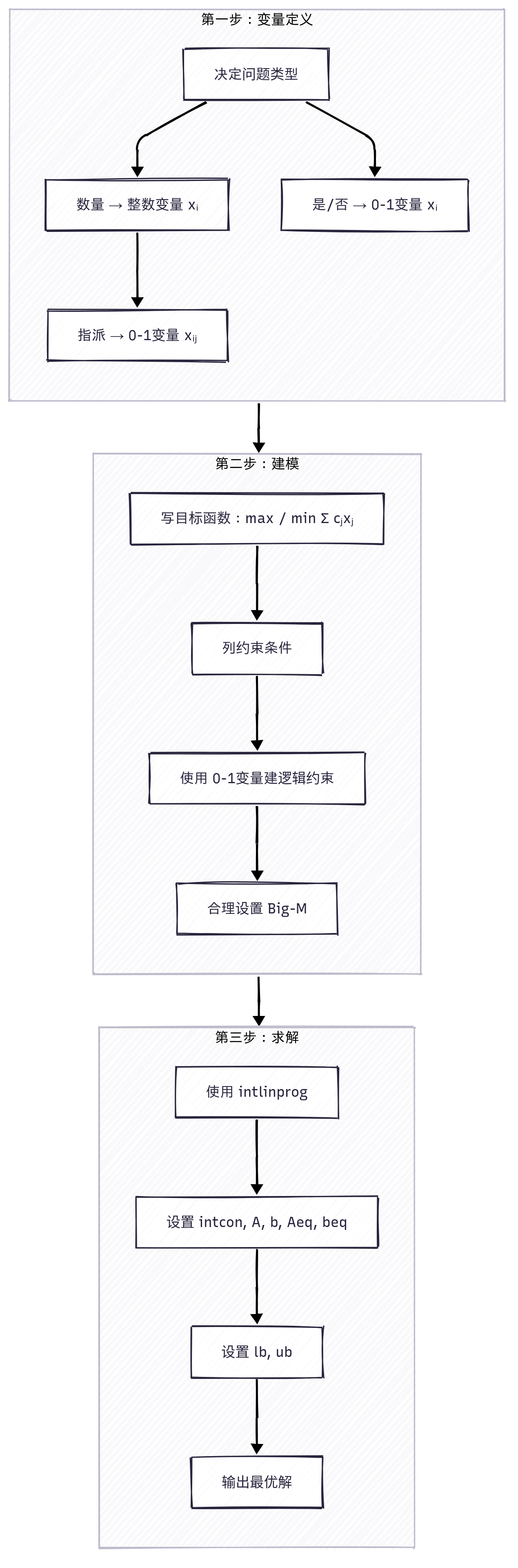
计算流程图
计算流程图

第一步：问题识别、变量定义

这一步的方法与【数模学习笔记】线性规划（LP）的原理和过程详解中介绍的方法很相似，此处精简叙述。

变量定义得好，模型就成功了一半。

先问自己一句话：我到底要决定什么？

  • 数量类决策：如果是决定“要多少”，比如生产多少件、分配多少台设备，就用整数变量 $x_i$。
  • 是/否类决策：如果是决定“要不要”，比如要不要建学校、要不要选某个方案，就用0-1变量。 例如：小学选址问题中，$x_i = 1$ 表示在 $B_i$ 建学校，$x_i = 0$ 表示不建。
  • 匹配/指派类决策：如果是决定“谁配给谁”，比如哪个工人干哪份活、哪台机器做哪个任务，就用带两个下标的0-1变量 $x_{ij}$。 例如：设备分配问题中，$x_{ij} = 1$ 表示第 $i$ 台设备分给第 $j$ 个企业。

变量定义一定要清楚。

如果全部变量都要求为整数，则称为纯整数规划；如果部分变量为整数，部分为连续变量，则称为混合整数规划。

第二步：目标函数、约束

这一步的方法与【数模学习笔记】线性规划（LP）的原理和过程详解中介绍的方法很相似，此处精简叙述。

  1. 目标函数： $$ \min \text{ or } \max Z = \sum_{j=1}^{n} c_j x_j $$ 其中 $c_j$ 是与决策变量 $x_j$ 相关的成本或收益系数。

  2. 约束条件

    建模的难点。将问题的限制翻译成不等式或等式。

    • **资源/容量约束：**最常见，通常是简单的线性不等式。例如，总运输重量不能超过卡车最大载重，总投资额不能超过预算上限。在大师兄视频里的背包问题中，这就是 $\sum \text{weight}_i \cdot x_i \le 30$

      巧用 0-1 变量 0-1 变量的强大之处在于：它能把各种“如果…那么…”、“只能选一个”、“至少选一个”这类逻辑条件变成线性约束。这里是建模难点。

      常见套路：

      逻辑条件 数学写法 说明
      若…则… $y \ge x$ $x=1$ 时逼 $y=1$；$x=0$ 时不限制 $y$。
      互斥 $\sum x_i \le 1$ 最多只能选一个。
      至少一个 $\sum x_i \ge 1$ 至少选一个（小学选址覆盖条件常用）。
      固定成本 $y \le M\delta$，目标加 $F\delta$ $\delta$ 表示是否生产；产量>0 时自动触发固定成本。

      逻辑→0-1变量→线性约束

      关于 Big-M 约束 在上表的固定成本约束里，$y \le M\delta$ 是关键，就是 Big-M 方法。 不要随便写一句“令 $M$ 很大”，不严谨。要根据实际问题算出合理的 $M$，比如：

      “$M$ 是一个足够大的常数。根据工厂最大产能（或市场最大需求等物理限制），我们得出 $y$ 的上界为 [具体数值]，因此取 $M = [具体数值]$。这个值既足够大，又不会太大，从而保持模型紧致，提高求解效率。”

      选个“刚刚好大”的 $M$，能让模型跑得更快，也能体现建模细节。

第三步：模型求解

我使用MATLAB，求解混合整数线性规划的核心函数是 intlinprog。它和LP的 linprog 类似，但多了一个参数（来指定整数变量）。

函数原型：

[x, fval] = intlinprog(f, intcon, A, b, Aeq, beq, lb, ub)

参数详解：

参数 对应模型部分 解释说明
f 目标函数系数 $c$ 求解 $\min f^T x$。如果是最大化问题 $\max c^T x$，则令 f = -c，最后将结果 fval 取反。
intcon 整数变量索引 一个向量，用于指定哪些决策变量是整数。例如，intcon = [1,3] 表示变量 $x_1$ 和 $x_3$ 必须是整数。
A, b 不等式约束 $A x \le b$ A 是系数矩阵，b 是右端向量。
Aeq, beq 等式约束 $A_{eq} x = b_{eq}$ Aeq 是系数矩阵，beq 是右端向量。
lb, ub 变量的下界和上界 lb和 ub。对于0-1变量，这是至关重要的一步，需要将其下界设为0，上界设为1。

以下是一个来自大师兄视频中的完整代码示例，已经加上注释：

问题：

$$ \max \quad 40x_1 + 30x_2 \\ \text{s.t.} \quad \begin{cases} x_1 + x_2 \le 6 \\ 240x_1 + 120x_2 \le 1200 \\ x_1 \ge 1, x_2 \ge 1 \\ x_1, x_2 \text{为整数} \end{cases} $$

MATLAB代码：

% 目标函数: max 40x1 + 30x2  =>  min -40x1 - 30x2
f = [-40; -30];

% 指定整数变量: x1和x2都是整数
intcon = [1, 2];

% 不等式约束: A*x <= b
% x1 + x2 <= 6
% 240x1 + 120x2 <= 1200
A = [1, 1; 240, 120];
b = [6; 1200];

% 等式约束: Aeq*x = beq (本题没有)
Aeq = [];
beq = [];

% 变量上下界: lb <= x <= ub
% x1 >= 1, x2 >= 1
lb = [1; 1];
ub = []; % 无上界

% 调用求解器
[x, fval] = intlinprog(f, intcon, A, b, Aeq, beq, lb, ub);

% 显示结果
optimal_solution = x
% 由于是最大化问题, 目标值需要取反
max_profit = -fval

经典IP模型应用

很多复杂问题的核心，都能抽象成几个常见的模型。简要举例：

  • 0-1 背包问题 有若干物品（重量 $w_j$，价值 $v_j$），背包容量 $C$，问怎么选物品让价值最大且不超重。 $$ \max \sum_{j} v_j x_j \quad \text{s.t.} \quad \sum_{j} w_j x_j \le C, \quad x_j \in {0, 1} $$

  • 指派问题 $n$ 个人做 $n$ 个任务，每个任务给每人分配的成本不同。要一人一任务，总成本最小。 $$ \min \sum_{i} \sum_{j} c_{ij} x_{ij} \ \sum_{j} x_{ij} = 1, \quad \sum_{i} x_{ij} = 1, \quad x_{ij} \in {0, 1} $$

  • 集合覆盖问题 若干候选位置可建消防站，每个站能覆盖一些社区。目标是用最少的站覆盖所有社区。 $$ \min \sum_{j} x_j \quad \text{s.t.} \quad \sum_{j \in S_i} x_j \ge 1, \quad x_j \in {0, 1} $$

复杂问题 → 找对应的经典模型 → 加细节约束

模型的优缺点

优点

  1. 表达力强：能精确描述离散决策、逻辑条件、固定成本等真实场景，比纯线性规划更贴近现实。
  2. 全局最优：可找到并证明全局最优解，比启发式算法更可靠。
  3. 应用广：工业、金融、交通、通信等都有成熟应用。

缺点

  1. 计算复杂：变量多时求解时间会指数级飙升。
  2. 建模敏感：模型紧不紧（LP 松弛的“松”或“紧”）极大影响求解效率。不当的 Big-M 等松散写法会让分支定界树暴涨。（高手和新手的差距就在这里）。
  3. 依赖求解器：难用简单算法替代。

我的思考与总结

成败很多取决于定义变量时候的巧思。在这题里面，重要的是要运用0-1变量和Big-M等技巧，把逻辑关系转化为成线性约束，大师兄视频里的案例就是一种翻译练习。

整数规划 vs. 其他模型：

模型类型 适用场景 论文写法简要示例
LP 决策变量连续（比如产量、资金分配），且目标与约束均为线性。 “本问题的决策变量为连续可分的数量，且目标函数与约束条件均为线性，因此采用线性规划模型求解高效且合理。”
IP 决策变量离散（比如台数、人数、是否选择），包含逻辑条件，需要全局最优解。 “由于问题涉及不可分割的决策单元及复杂逻辑约束，并需获得可证明的最优解，因此构建混合整数线性规划模型。”
启发式算法（遗传算法、模拟退火等） 问题规模极大，IP 求解器在合理时间内无法精确求解，可接受高质量近似解。 “问题规模巨大，若直接构建整数规划模型将产生数十万级变量、约束，在有限时间内难以求得精确最优解。因此采用启发式算法（如遗传算法）快速搜索高质量可行解。”

敏感性分析

  • 做：挑一个关键参数（如背包容量、预算、关键人员时间），让它在合理范围内变化，重新求解模型，看最优值和最优方案怎么变。

  • 展示：画图 + 文字解释。 比如：

    对货车容量做敏感性分析，结果如图 X。容量从 25 吨增至 35 吨时，利润几乎线性增长，每多 1 吨约多赚 80 元。但超过 35 吨后增长趋缓，因为高价值货已装满。 结论：将容量升到 35 吨是最划算的，再加就不经济了。

参考资料

【大师兄数学建模】第8讲 整数规划_哔哩哔哩_bilibili

【数模学习笔记】整数规划（IP）的原理和过程详解
https://blog.kylinoio.fun/index.php/archives/28/
本文作者 KylinOIO
发布时间 2025-08-01
许可协议 CC BY-NC-SA 4.0
发表新评论
0:00