【数模学习笔记】灰色关联分析(GRA)的原理和过程详解
=## 前言和简述
这个模型是用来解决什么问题的?
- 在很多个影响因素中,找出对目标影响最大(最关键)的因素。
- (较不常用)当有多个备选方案,每个方案又有多个评价指标时,可以用来判断哪个方案与最理想方案的趋势最接近,来选出最优方案。
为什么需要学习这个模型?它在数学建模中的地位或常用性如何?
- 对数据要求极低:即使只有4、5个数据点也能进行分析。不要求数据服从特定概率分布,适用性极强。
- 原理直观,计算简单:整个计算过程只涉及简单的加减乘除和求最值。
- **结果清晰,解释性强:**模型输出具体的数值,可以直接用来比较。
- 专为“灰色系统”设计:信息不完全、不明确的系统(尤其是经济、社会领域)。
解决评价、排序、决策类问题,最常用的:AHP、TOPSIS、GRA。
AHP偏主观,依赖专家打分。
TOPSIS和GRA偏客观,依赖原始数据。
大家经常结合使用它们,比如用AHP确定各指标的权重,再用GRA或TOPSIS进行具体方案的评价排序,主客观结合。
原理和计算步骤
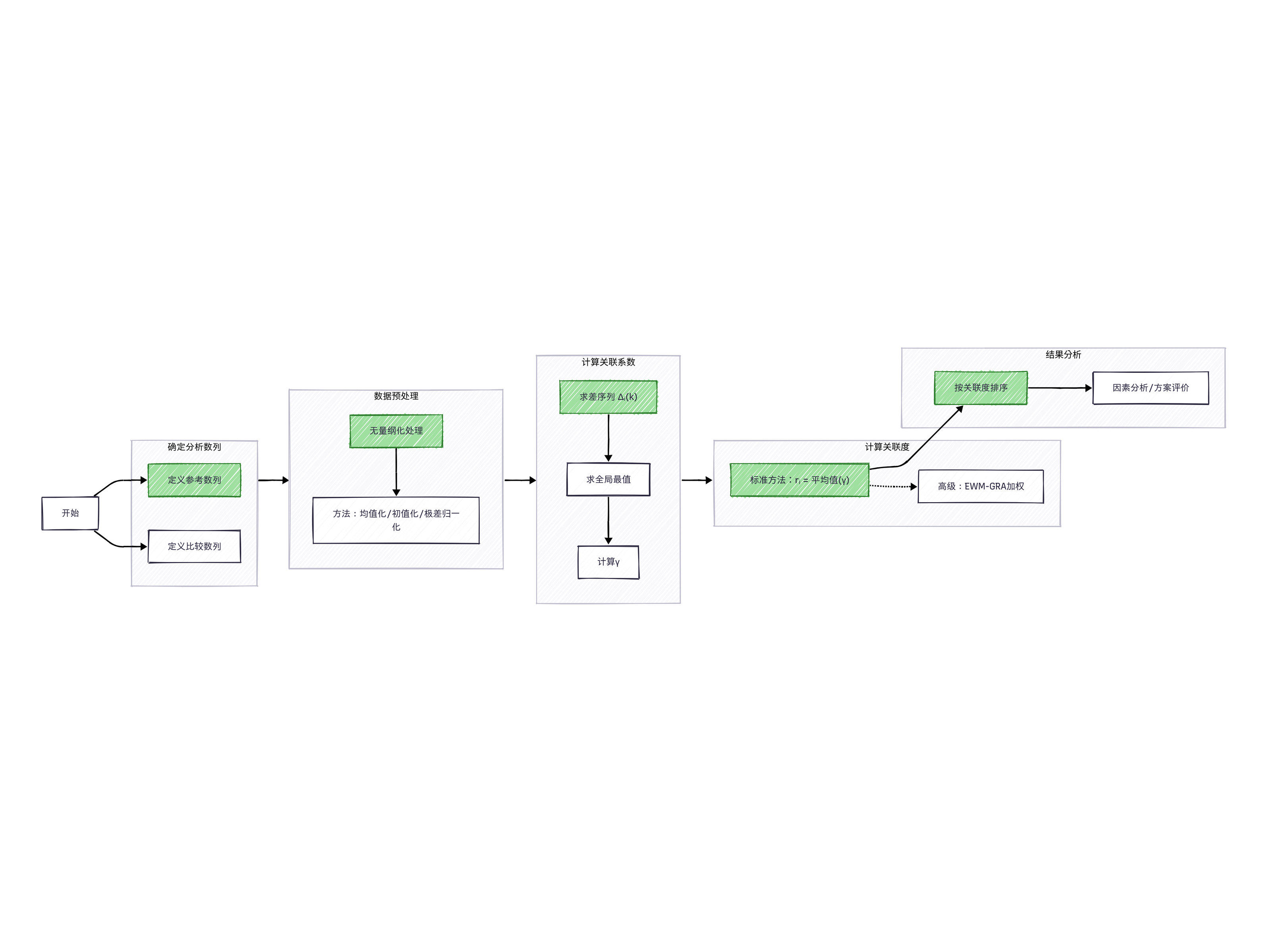
计算流程图:
确定分析数列
先确定两个数列:
-
参考数列(母序列),记作 $x_0$:代表最关心的结果,类似因变量。。
-
比较数列(子序列),记作 $x_i (i=1, 2, ..., m)$:由影响系统行为的各个因素构成,类似自变量。
如果是综合评价类问题,参考数列一般是构建一个“虚拟最优参考列”来确定(序列的每一个值都是所有待评价对象在对应指标上的最优值)。最后的结果最接近这个虚拟参考列就是最优。
数据预处理
必须对原始数据进行无量纲化处理,使不同量纲可以比较。
数据的无量纲化与标准化的具体方法与【数模学习笔记】熵权法(EWM)的原理和过程详解中介绍的方法完全相同,此处不赘述。常用的方法包括均值化、初值化或极差归一化等。
方法选择的阐述
不同方法对最终排序影响不同。优秀论文不会仅仅说“我们对数据进行了标准化”,而会阐述原因。
比如可以类似这样写:“考虑到本问题旨在比较各方案的相对优劣,我们选用了极差归一化方法。该方法能将所有指标数据线性地映射到
[0, 1]区间,既消除了量纲影响,又最大限度地保留了原始数据在各个指标内的相对分布关系,便于后续几何形状的比较。我们注意到,不同的无量纲化方法可能导致结果的细微差异,但对于本问题的评价目标而言,极差归一化是最为直观和恰当的选择。”这样可以体现对模型细节的思考,还有稳健性,是评委希望看到的深度。
计算灰色关联系数
关联系数衡量比较数列与参考数列曲线的接近程度。
-
求差序列:计算每个比较数列 $x_i$ 在第 $k$ 个点上与参考数列 $x_0$ 的绝对差值。记为 $\Delta_i(k) = |x_0(k) - x_i(k)|$。
-
求两级最值:在所有差值中,找出全局的最大值和最小值。
- 全局最小值:$$m = \min_{i} \min_{k} \Delta_i(k)$$
- 全局最大值:$$M = \max_{i} \max_{k} \Delta_i(k)$$
-
计算关联系数:计算每个点 $k$ 的灰色关联系数 $\gamma(x_0(k), x_i(k))$:$$ \gamma(x_0(k), x_i(k)) = \frac{m + \rho M}{\Delta_i(k) + \rho M} $$ 其中$\rho$ 是分辨系数,取值范围 $(0, 1)$。
**分辨系数 $\rho$ **
$\rho$ 的作用:它用于调节关联系数之间的“对比度”。
- $\rho$ 越小,关联系数间的差异越大,分辨能力越强;
- $\rho$ 越大,关联系数间的差异越小,分辨能力越弱,但整体的稳定性更好。
在绝大多数论文中,$\rho$ 通常直接取值为 0.5,比较常规的做法。
高级技巧:对 $\rho$ 进行灵敏度分析:直接取 $\rho=0.5$ 比较主观。顶尖论文会进行灵敏度分析,来证明其结论的稳健性(结论不因 $\rho$ 的主观取值而改变)。更有说服力更专业。具体做法:
- 将 $\rho$ 从 0.1 到 0.9 以 0.1 为步长进行遍历。
- 对每一个 $\rho$ 值,都完整计算出所有比较数列的最终灰色关联度。
- 绘制一张以 $\rho$ 为横轴、灰色关联度为纵轴的折线图。图中的每一条线代表一个比较数列(或评价方案)。
- 分析这个图,如果主要因素(或最优方案)的排序在整个 $\rho$ 的取值范围内保持稳定(即对应的几条折线没有发生交叉),就可以在论文中自信的写:“为检验模型结果的稳健性,本文对分辨系数 $\rho$ 进行了灵敏度分析。如图X所示,当 $\rho$ 在 $[0.1, 0.9]$ 区间内变化时,各主要因素的关联度排序保持不变。这表明本文的结论具有高稳健性,不受分辨系数主观取值的影响。”
计算灰色关联度
将前面计算出的各个点的关联系数进行综合。
- 标准方法:直接求算术平均值最常见(简单直观,适用许多场景)。比较数列 $x_i$ 与参考数列 $x_0$ 的灰色关联度 $r_i$ 为: $$ r_i = \frac{1}{n} \sum_{k=1}^n \gamma(x_0(k), x_i(k)) $$
高级技巧:EWM-GRA组合模型
刚刚说的标准方法,隐含假设:每个评价指标的重要性完全相同。但是,现实中,各个指标的权重往往不同。举例来说,评价供应商时,“产品质量”的权重应该高于“售后服务响应时间”。
引入熵权法会更科学客观,很加分,有关熵权法可见
【数模学习笔记】熵权法(EWM)的原理和过程详解。先用熵权法计算出第 $k$ 个指标的权重 $w_k$ 。然后使用加权平均来计算灰色关联度: $$ r_i = \sum_{k=1}^n w_k \cdot \gamma(x_0(k), x_i(k)) $$ 其中,$$ \sum_{k=1}^n w_k = 1 $$
在论文里可以类似这样写:“传统灰色关联分析模型在计算关联度时采用等权重均值,未能体现各评价指标间的差异性。为使评价结果更加客观科学,本文引入熵权法对模型进行改进。使用熵权法确定各指标的客观权重,并以此权重对各点的关联系数进行加权求和,构建了EWM-GRA组合评价模型。该模型能够充分利用数据自身的信息,减少由主观赋权的随意性,使决策更可靠。”
关联度排序与分析
最后一步,根据计算出的灰色关联度 $r_i$ 得出结论。
- 排序:将所有比较数列(或评价方案)按照其灰色关联度 $r_i$ 的大小降序。
- 分析与结论:关联度数值越大,表示对应的比较数列与参考数列的关联性越强(也可以说是对应的评价方案与最优方案越接近)。
- 用于因素分析:“根据表2的灰色关联度计算结果,影响结婚对数的主要因素排序为:女性失业数($r_3 = 0.8924$)> 房价($r_1 = 0.5895$)> 人均收入($r_2 = 0.5696$)。这表明,在所分析的因素中,女性就业保障问题对年轻人结婚意愿的影响最大,其次是高昂的房价。”
- 用于综合评价:“各备选供应商的综合评价结果如表2所示,其灰色关联度排序为:供应商4 > 供应商6 > 供应商2 >...。因此,供应商4与虚拟最优供应商的关联度最高,是本次采购的最优选择。”
模型的优缺点
优点
-
对数据要求低:无需大量样本,对数据分布没有严格要求,适用性广。
-
计算简便,原理直观:模型的核心思想是比较几何形状相似度,易于解释。
-
有效处理共线性问题:传统回归分析中,多重共线性会严重影响模型结果。而GRA是逐一分析各因素与参考目标的关系,从根本上规避了这个问题。
-
结果清晰:可以直接用于因素重要性排序。
缺点
-
存在主观性:分辨系数 $ρ$ 的取值是人为设定的。所以灵敏度分析很重要,弥补这一不足。
-
对参考序列敏感:尤其在评价问题中,虚拟最优参考序列的构建方式会影响最终排序。所以必须清晰论证其构建的合理性。
-
对预处理方法敏感:如前所述,不同的无量纲化方法可能导致结果差异,这也是模型的一个潜在不确定性来源。
-
提供相对关系,而非绝对关系:GRA给出的关联度只能用于排序。例如,关联度为0.8并不意味着其影响程度是关联度为0.4的两倍。不是像回归系数那样明确的、绝对的量化意义。
我的思考与总结
GRA在数学建模中的定位
GRA的最佳应用场景:数据质量不高、样本量不足,且无法满足传统统计模型(如回归分析、方差分析)的严格假设时。
也可以作为其他复杂模型的前置步骤。例如,可以先用GRA从十几个潜在影响因素中筛选出最重要的三到四个,然后再将这几个筛选出的变量作为输入,去构建一个更复杂的预测模型(如神经网络、时间序列模型等)。更有逻辑。
拥抱组合模型
单一基础的模型很难脱颖而出。所以最好组合不同模型,取长补短。
参考资料
【大师兄数学建模】第6讲 灰色关联分析_哔哩哔哩_bilibili