【数模学习笔记】TOPSIS法 (优劣解距离法) 的原理和过程详解
前言和简述
这个模型是用来解决什么问题的?
如果需要从一堆选项中,根据一套标准,科学地选出最优的那个,TOPSIS法就很适合。
为什么需要学习这个模型?它在数学建模中的地位或常用性如何?
TOPSIS的应用广泛:内在逻辑的直观、计算过程的简便。对于向评委阐述模型时具有天然的优势,可以清晰传达建模思路
TOPSIS也很少独立出现,如果单独使用基础的TOPSIS就太浅显了。经典的组合:熵权法-TOPSIS模型 (熵权法客观地计算出各指标的权重,TOPSIS模型用这些权重来对所有备选方案进行排序)。
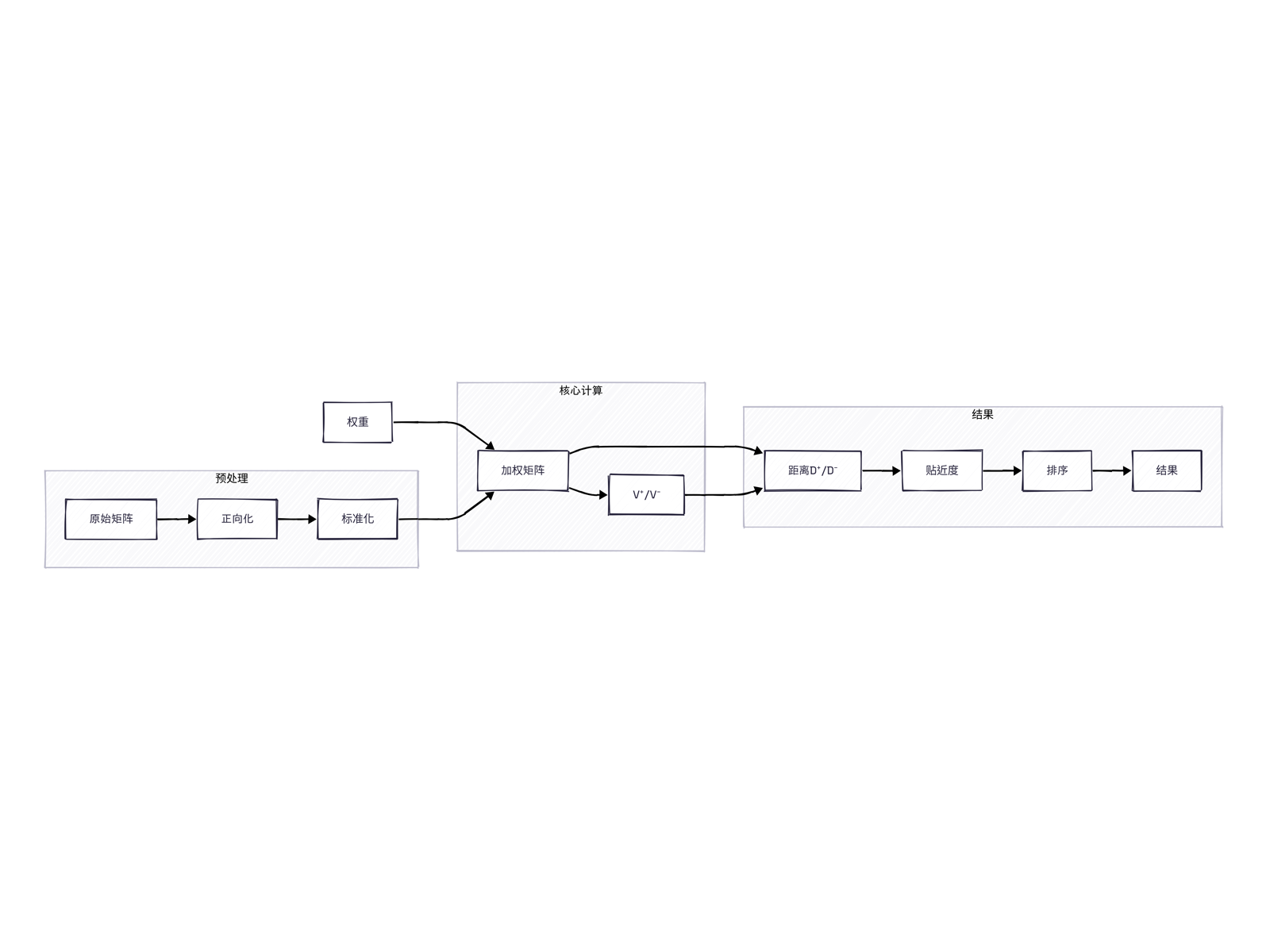
原理和计算步骤
计算流程图:
设原始评价矩阵 $X$,其中 $n$ 个待评价对象(行)和 $m$ 个评价指标(列):
$$ X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix} $$ 其中 $x_{ij}$ 表示第 $i$ 个对象在第 $j$ 个指标下的原始数值。第一步:指标正向化
进行数据预处理,确保所有指标的方向性相同(数值越大越优)。
TOPSIS的指标正向化方法与【数模学习笔记】熵权法(EWM)的原理和过程详解中指标正向化的方法完全相同,这里不赘述。
这里的关键是展现建模严谨性。在论文里,不要默默地处理数据。必须明确列出每一个评价指标,并清晰说明类型(极大、极小、中间型、区间型),然后论证为什么选择相应的正向化公式。
可以基于行业标准、数据分布特征。展示理解。
第二步:数据标准化
TOPSIS的数据标准化方法与【数模学习笔记】熵权法(EWM)的原理和过程详解中指标正向化的方法完全相同,这里不赘述(注意:TOPSIS可以不对0值进行处理,TOPSIS不怕0)。
第三步:构建加权标准化矩阵
通过别的方法获取到的权重向量 $W = [w_1, w_2, \dots, w_m]$,其中 $w_j$ 是第 $j$ 个指标的权重,且满足 $\sum_{j=1}^{m} w_j = 1$。如前所述,$W$最好通过熵权法之类的客观赋权方法得到。
标准化矩阵 $Z$ 与权重向量 $W$ 相乘,得到加权标准化矩阵 $V$
$$ v_{ij} = w_j \times z_{ij} $$ $V$同时代表了每个方案在各个指标上的相对表现( $z_{ij}$ )和各个指标本身相对重要性( $w_j$ )。第四步:确定正理想解V+与负理想解V-
核心思想:基于几何空间中的距离概念。我们先可以定义出两个当做基准的最极端的方案:
-
正理想解$V+$:理论最佳方案,在每一个评价指标上都取的最优值。 $$ V^+ = (v_1^+, v_2^+, \dots, v_m^+) = (\max_{i}{v_{i1}}, \max_{i}{v_{i2}}, \dots, \max_{i}{v_{im}}) $$
-
负理想解$V−$:理论最差方案,在每一个评价指标上都取的最劣值。 $$ V^- = (v_1^-, v_2^-, \dots, v_m^-) = (\min_{i}{v_{i1}}, \min_{i}{v_{i2}}, \dots, \min_{i}{v_{im}}) $$
第五步:计算距离
对于每一个方案,分别计算它与$V+$和$V-$的距离。越靠近$V+$,同时越远离$V-$,那它就越优。从而方便下一步可以给所有方案排序。
-
第 $i$ 个备选方案到**正理想解V+**的距离 $D_i^+$: $$ D_i^+ = \sqrt{\sum_{j=1}^{m}(v_{ij} - v_j^+)^2} $$
-
第 $i$ 个备选方案到**负理想解V-**的距离 $D_i^-$: $$ D_i^- = \sqrt{\sum_{j=1}^{m}(v_{ij} - v_j^-)^2} $$
第六步:计算相对贴近度并排名
给每个备选方案算出一个综合评价指数,称为相对贴近度,记为 $S_i$,公式如下:
$$ S_i = \frac{D_i^-}{D_i^+ + D_i^-} $$- $S_i$ 的取值范围在 $[0, 1]$ 之间。
- 如果一个方案非常接近V+,则 $D_i^+$ 会很小;如果它同时又远离Z-,则 $D_i^-$ 会很大。这种情况,$S_i$ 的值会趋近于1。
- 反之,如果一个方案远离V+($D_i^+$ 很大)且靠近Z-($D_i^-$ 很小),这种情况 $S_i$ 的值会趋近于0。
因此,$S_i$ 的值越大,代表该备选方案的综合表现越优。最后,将所有方案按照 $S_i$ 的值从大到小进行排序,即可得到最终的评价结果。
模型的优缺点
优点
-
**逻辑清晰,计算简单:**TOPSIS基于直观的几何概念,计算步骤很固定,不涉及复杂的优化过程。
-
**结果精确:**模型输出分数,一目了然,没有歧义。即使有大量备选方案和评价指标,计算流程的步数也不变。
-
应用广泛:对数据类型要求不高,定量数据或经过适当量化处理的定性数据,都可以评价。
缺点
-
排序反转问题:TOPSIS最广为人知的理论缺陷。增或删一个(即使是无关紧要的)备选方案之后,原有的方案之间的排序可能改变 。主要是因为,V+和V-是根据当前数据集中的最大值和最小值来定义的。一旦数据集变动,V+和V-就会漂移,导致所有方案到这两个点的距离都要重新算,导致(可能)排序错乱。
在论文中,可以说:“我们注意到,传统TOPSIS模型的评价基准(正负理想解)依赖于数据集本身,这可能导致排序反转问题。为了验证我们结论的稳定性,我们进行了稳健性分析……”
-
指标相关性问题:标准的TOPSIS模型在计算D时用欧几里得距离。这隐含了一个假设,说决策空间中的各个坐标轴(评价指标)相互独立、相互正交 。但是指标间常有相关性,在实际中。比如,评价企业创新能力时,“研发投入金额”和“专利申请数量”这两指标高度正相关。如果直接都纳入模型,会无形中重复计算“创新投入”这一潜在影响力,导致结果扭曲。
更厉害的论文可以指出这个问题,并提出解决方案,类似:“考虑到指标间可能存在的共线性问题,我们首先采用主成分分析对原始指标体系进行降维,提取出相互独立的主成分,再将这些主成分作为新的评价指标输入TOPSIS模型,从而避免信息冗余对评价结果的干扰。”
-
权重主观性:TOPSIS不提供确定指标权重的方法。如果权重是决定得很主观,那就不太科学了,容易丢分。就是为什么熵权法-TOPSIS这个组合如此的好,熵权法是客观的,完美弥补了这哥短板。
我的思考与总结
学习TOPSIS的核心
TOPSIS的计算本身很简单,真正拉开差距的在于对模型的理解、批判性审视。
把重心放在:
- 合理性:为什么选择这些指标?为什么这样进行正向化处理?为什么采用这种赋权方法?每一个决策都需要在论文中有理有据地呈现。
- 结果解读:得到的排名意味着什么?它是否符合常识或问题的内在逻辑?如果出现反直觉的结果,是什么样的数据特征导致了这种现象?模型的结论是否稳健?
建模竞赛注意事项与小妙招
-
论证:在论文中介绍模型时,务必以一段话清晰地阐述选择TOPSIS的理由。
比如类似:“本问题旨在对N个供应商的综合表现进行排序,属于典型的多属性决策问题。考虑到评价指标多为定量数据,且需要一个明确客观的排序结果,我们选用TOPSIS作为核心评价模型。该模型原理直观,能综合各指标信息,得出唯一的优劣次序。为保证评价的客观性,我们进一步引入熵权法来确定各指标权重,构建了熵权法-TOPSIS评价模型。”
-
可视化:
-
权重可视化:使用柱状图展示由熵权法计算出的各指标权重。图表下方必须配有文字解读。
比如:“如图X所示,指标‘供货稳定性’的权重(0.48)远高于其他指标,这表明在本次评估的数据集中,各供应商在该指标上的表现差异最大,因而蕴含了最多的决策信息,对最终排名起到了决定性作用。这一发现与企业高度重视供应链管理中的稳定,和现实情况相符。”
-
排名可视化:同样使用柱状图展示最终排名前列的方案及其TOPSIS得分。
-
-
稳健性分析(敏感性分析):做稳健性分析,也是正面回应模型“排序反转”的问题,写了的话优秀论文概率会高很多(说明我们的模型很可靠)。
-
方法:扰动模型中的不确定性因素,观察结果够不够稳定。最常见的是对权重进行扰动。比如把熵权法计算出的每个权重分别增加10%,同时按比例减少其他权重以保证总和为1,然后重新跑一下TOPSIS。也可以随机剔除一小部分样本(比如5%的数据)后重新跑一次。
-
结果呈现:在论文中用一个简洁的表格来展示分析结果。
类似这样:
表X:模型稳健性分析
扰动情景 第一名 第二名 第三名 第四名 ... 基准线 (原始权重) 方案A 方案C 方案D 方案B ... 指标1权重增加10% 方案A 方案C 方案D 方案B ... 指标2权重增加10% 方案A 方案D 方案C 方案B ... 随机剔除5%样本 方案A 方案C 方案B 方案D ... “为了检验模型结果的可靠性,我们进行了权重敏感性分析。如表X所示,尽管各指标权重发生了±10%的扰动,排名前两位的方案(方案A和方案C)始终保持其领先地位。这表明我们的评价结果具有较强的稳健性,最终推荐‘方案A’作为最优选择的结论是可靠的,并非特定权重下的偶然产物。”
-
参考资料
【大师兄数学建模】第5讲 Topsis_哔哩哔哩_bilibili
2021年国赛C题优秀论文. (2021). 生产企业原材料订购与运输的评价与规划模型.
刘明月. (2021). 基于熵权-Topsis的江西电子信息产业集群出口方式选择研究. 南昌大学.