【数模学习笔记】熵权法（EWM）的原理和过程详解

前言和简述

这个模型是用来解决什么问题的？

熵权法完全根据数据本身来确定各个评价指标的权重。为各项指标合理地分配权重，避免主观。

当需要对多个方案、对象或年份进行综合评价的问题。通常涉及一个包含n个评价对象和m个评价指标的原始数据矩阵。熵权法的任务就是为这m个指标中的每一个计算出一个权重，反映信息量的大小 。

为什么需要学习这个模型？它在数学建模中的地位或常用性如何？

如果题目给出了明确的评价数据，但没有任何关于指标重要性的先验知识或专家意见时，熵权法就很好，比较严谨的、客观的。EWM告诉我们哪个指标最具区分度。最终的决策还得靠依赖下游的评价模型。

熵权法有很好的生态，它本身很少作为独立出现。它更常见的角色是作为一个前置的计算，其计算出的权重来服务更复杂的综合评价模型。经典的组合：熵权法-TOPSIS模型 （熵权法客观地计算出各指标的权重，TOPSIS模型用这些权重来对所有备选方案进行排序）。熵权法计算出的权重也可以与灰色关联分析（GRA）、模糊综合评价（FCE）或简单的加权求和法结合，更完整评价体系。

原理

核心思想：一个指标的数据序列离散程度越大（即方差或变异性越大），则该指标所蕴含的有效信息就越多，对评价结果的区分能力就越强，因此应被赋予更高的权重 。

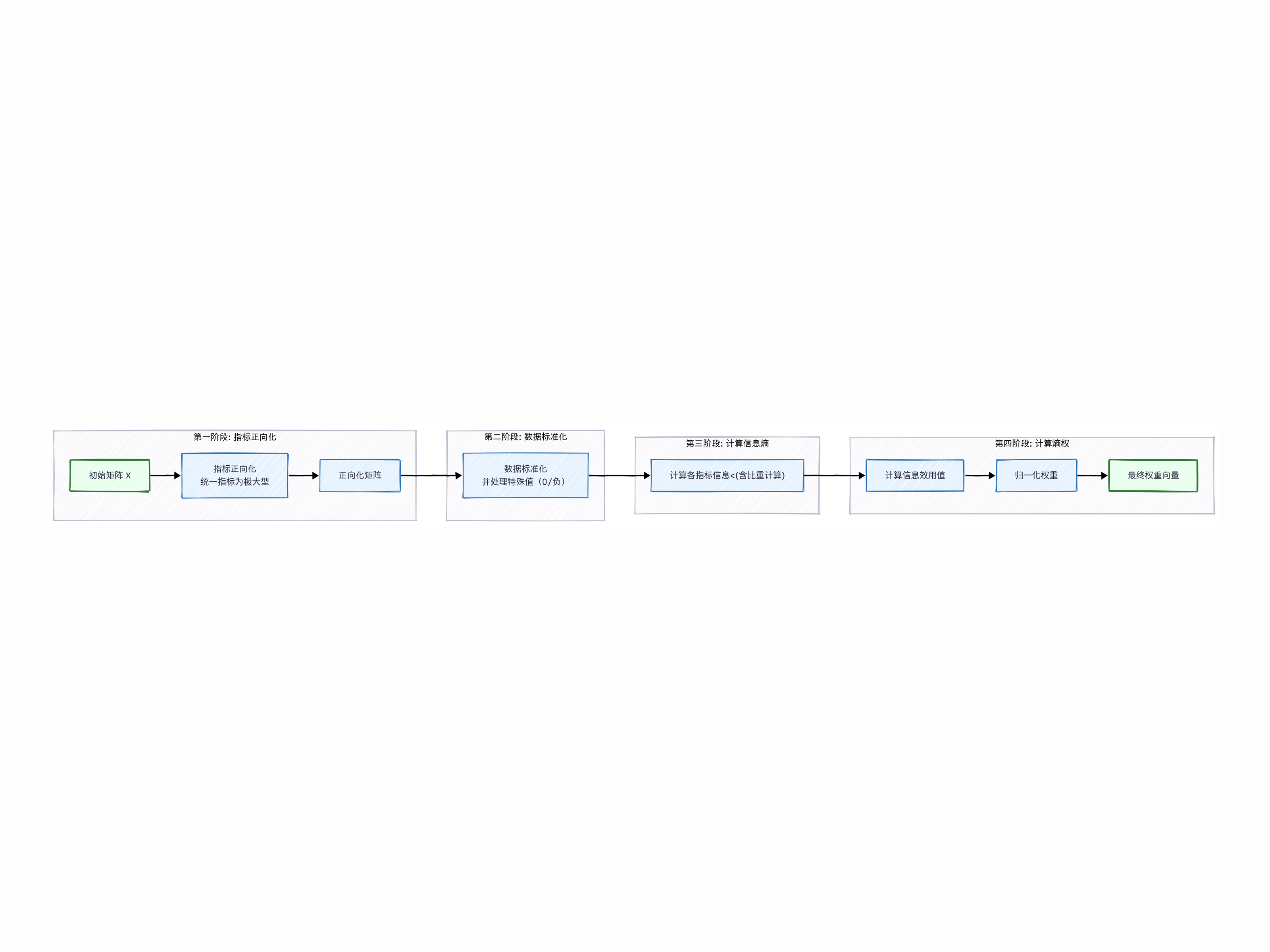
逻辑过程如下图：

计算步骤

计算流程图：

假设存在一个初始评价矩阵 X，其中包含 n 个待评价对象（行）和 m 个评价指标（列）：

$$ X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix} $$ 其中$$x_{ij}$$ 表示$$i$$个对象在第$j$个指标下的原始数值。

第一步：指标正向化

确保对于每个指标，数值越大代表越优。这是进行跨指标比较和加权的前提。

不同类型的指标需要不同的正向化方法。必须深刻理解问题后设定这些参数（正向化公式的选择，特别是其中参数（比如最佳值 $x_{\text{best}}$、最佳区间 $[a, b]$) 的确定）），并在论文中明确说明其选择依据。

常见指标类型的正向化公式：

指标类型	特点	举例	正向化公式
极大型 (效益型)	数值越大越好	GDP、收入、分数	无需处理, 或保持 $x'{ij} = x{ij}$
极小型 (成本型)	数值越小越好	污染指数、成本、故障率	$x'{ij} = \max(x_j) - x{ij}$ 或 $x'{ij} = \frac{1}{x{ij}}$ (要求 $x_{ij} > 0$)
中间型	数值越接近某个特定值 $x_{best}$ 越好	pH值、水温、身高	$M = \max{
区间型	数值落在某个最佳区间 $[a, b]$ 内最好	体温、湿度	$M = \max{\max_i{x_{ij}} - b, a - \min_i{x_{ij}}}$ $x'{ij} = \begin{cases} 1 - \frac{a - x{ij}}{M}, & x_{ij} < a \ 1, & a \le x_{ij} \le b \ 1 - \frac{x_{ij} - b}{M}, & x_{ij} > b \end{cases}$

第二步：数据标准化

设有$n$个评价对象, $m$个评价指标（已正向化）， 构成矩阵：

$$ X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix} $$ 设标准化的矩阵为Z，那么Z中的每一个元素: $z_{ij} = \frac{x_{ij}}{\sqrt{\sum_{i=1}^{n} x_{ij}^2}}$

如果其中有负元素，则令$\tilde{z}{ij} = \frac{x{ij} - \min{x_{1j}, x_{2j}, \cdots, x_{nj}}}{\max{x_{1j}, x_{2j}, \cdots, x_{nj}} - \min{x_{1j}, x_{2j}, \cdots, x_{nj}}}$

得到标准化矩阵$\tilde{Z} = \begin{bmatrix} \tilde{z}{11} & \tilde{z}{12} & \cdots & \tilde{z}{1m} \ \tilde{z}{21} & \tilde{z}{22} & \cdots & \tilde{z}{2m} \ \vdots & \vdots & \ddots & \vdots \ \tilde{z}{n1} & \tilde{z}{n2} & \cdots & \tilde{z}_{nm} \end{bmatrix}$

其实正向化后就可以保证标准矩阵不为负了，但为了严谨一些，我们还是按照书上讲解，代码里最好也加上判断逻辑。

处理0值和负数的特殊情况：

标准化后的矩阵 Z 中可能存在0值。在后续会引发问题。直接计算 0 * log(0) 会NaN。

实践中可以直接对标准化后的数据进行小小的平移。比如可以对整个矩阵 Z 进行如下变换： $$ z'{ij} = z{ij} + \epsilon $$

其中 $\epsilon$ 是一个极小的正数 (如 $10^{-6}$)。

想要更严谨的话可以直接在标准化公式中进行调整。比如 $$ z_{ij} = \frac{x'{ij} - \min(x'{j})}{\max(x'{j}) - \min(x'{j})} + \epsilon $$ 注意：如果一个指标的原始数据中有大量0值，可能会扭曲权重计算结果，让这个指标的权重高得不合理。

在论文中必须清晰说明处理0值的方法及其合理性。

第三步：计算指标信息熵

1. 计算比重矩阵 P：

   需要计算在第 $j$个指标下，第 $i$ 个对象的评价值占该指标所有评价值总和的比重。这个比重 $p_{ij}$ 可以被看作是一种“概率”的度量。 $$ p_{ij} = \frac{z_{ij}}{\sum_{i=1}^{n} z_{ij}} $$

   为避免分母为0，若某指标 $j$ 的所有标准化值 $z_{ij}$ 均为0，那个就应该直接被剔除，或赋予权重0。

2. 计算信息熵 $e_j$：

   对于每个指标 $j$，根据其比重数据计算信息熵。常数 $k = 1/\ln(n)$ 确保 $e_j$ 的取值范围在 $[0,1]$ 之间。 $$ e_j = -k \sum_{i=1}^{n} p_{ij} \ln(p_{ij}) = -\frac{1}{\ln(n)} \sum_{i=1}^{n} p_{ij} \ln(p_{ij}) $$

   在计算时，约定当 $p_{ij} = 0$ 时，$p_{ij} \ln(p_{ij}) = 0$。

第四步：计算熵权

1. 计算信息效用值 $d_j$： 信息熵越小，表示提供的信息越多，效用值就越大。 $$ d_j = 1 - e_j $$

2. 计算最终权重 $W_j$： 归一化处理后就是熵权（所有指标的权重之和为1）： $$ W_j = \frac{d_j}{\sum_{j=1}^{m} d_j} $$

最终熵权计算完毕。

案例详解

以简化的供应商评价问题为例。假设需要对4家供应商（A, B, C, D）基于3个指标（产品合格率、供货准时率、价格）进行评价。

原始数据矩阵 X：

供应商	合格率 (%) (极大型)	供货准时率 (%) (极大型)	价格 (元/件) (极小型)
A	99	95	10
B	98	98	12
C	99	92	11
D	96	95	9.5

第一步：指标正向化

• 合格率和准时率是极大型，无需处理。
• 价格是极小型指标，使用 $x'{ij} = \max(x_j) - x{ij}$ 进行正向化。$\max(\text{价格}) = 12$。
• 正向化后的价格：A: 12 − 10 = 2; B: 12 − 12 = 0; C: 12 − 11 = 1; D: 12 − 9.5 = 2.5。

第二步：数据标准化

正向化价格: min = 0, max = 2.5。

标准化矩阵 Z：

供应商	合格率	准时率	正向化价格
A	1.000	0.500	0.800
B	0.667	1.000	0.000
C	1.000	0.000	0.400
D	0.000	0.500	1.000

第三步和第四步：计算信息熵和熵权

指标	信息熵 eⱼ	信息效用值 dⱼ	最终权重 Wⱼ
合格率	0.898	0.102	0.102 / (0.102+0.150+0.285) = 0.209
准时率	0.850	0.150	0.150 / (0.102+0.150+0.285) = 0.308
价格	0.715	0.285	0.285 / (0.102+0.150+0.285) = 0.483

权重分别为：价格(0.483) > 供货准时率(0.308) > 产品合格率(0.209)。这表明，在当前这四家中，“价格”指标的差异性最大，最具区分度，因此获得了最高的权重。（这些权重可以用于接下来的计算，来得出最终的排名。）

模型的优缺点

优点

1. 客观：权重完全由数据驱动，增强说服力。
2. 简单，易于实现：可以方便地使用MATLAB、Python、Excel实现。
3. 适用性广：对数据类型没有苛刻要求，只要是能够量化的，原则上都可确定指标权重。

缺点

1. 忽略指标间的相关性：在计算每个指标的权重时，是独立地、逐列地进行的，完全忽略了指标间的关系。比如在评价区域经济发展时，“人均GDP”和“人均可支配收入”两个指标高度正相关，如果两个权重都很高，就这是对潜在的“经济富裕程度”的重复加权，导致不公正。
2. 忽略了等级区分度：比如一个指标下的得分为{100, 99, 1}，另一个指标{100, 50, 1}。两者产生的优劣排序完全相同（A>B>C），但后者的离散度远大于前者，因此后者权重高得多的。如果仅仅是排序，这种分配可能并不合理。
3. 对数据质量的极端依赖：Garbage in, garbage out。异常值会扭曲计算结果。如前所述，数据中存在的大量0值也会导致失真 。

我的思考与总结

学习熵权法的核心

学习熵权法的过程的核心，并非在于掌握复杂的数学推导，真正的拉开差距的地方在于：

1. 正向化方法的合理选择与论证：如何为中间型或区间型指标选择合适的正向化公式并确定其关键参数很重要，而且还需要再论文中表述清楚。
2. 对输出权重的批判性审视：不能将熵权法当成一个黑箱，盲目接受输出。必须结合实际问题背景，对合理性深入分析解读。如果结果与常识相悖，要能够解释数据为何导致这样的结果。

与其他模型的联系与区别

EWM和AHP的对比：

比较维度	熵权法	层次分析法
赋权哲学	客观赋权，数据驱动。权重是数据内在信息的体现。	主观赋权，专家驱动。权重是专家知识和偏好的量化。
数据要求	需要一个完整的定量数据矩阵（n个对象 × m个指标）。	无需矩阵，两两比较打分。
核心优势	排除人为偏见，结果可复现，有数据时说服力强。	能够融入专家经验、定性因素，更灵活。
核心劣势	忽略指标的相关性，对数据敏感。	依赖专家的公正性，构建过程繁琐，可能逻辑不一致。
口诀（	“有数据用熵权”：当题目提供现成的数据表时，优先EWM。	“没数据用层次”：当题目只给出定性描述，需要自己构建指标体系时，优先AHP。

建模竞赛注意事项与小妙招

1. 一定要论证：论文中必须对每一个关键步骤详尽论证。包括：为什么选择EWM（而不是AHP）、如何进行指标正向化（特别是参数的选取依据）、如何处理数据中的异常值和零值等。
2. 权重可视化与解读：不要只在表格中列数值。务必使用柱状图，让评委一目了然。而且更重要对图进行解读：这些权重分布是否符合直觉？如果出现反直觉的结果，要分析数据层面的原因（例如，“指标X虽然概念上重要，但在本数据集中区分度不大，因此权重较低”）。
3. 组合赋权模型：为了克服单一方法的局限性，可以尝试构建组合赋权模型。例如，分别用EWM和AHP计算出一套客观权重 Wobj 和主观权重 Wsubj，然后通过一个组合系数 α 将它们结合起来：Wfinal=α⋅Wobj+(1−α)⋅Wsubj。在论文中可以论证 α 的取值（如各取0.5，或根据问题性质有所侧重），或者分析最终评价结果对 α 变化的敏感性。可以很好展示我们对不同方法优劣的理解。
4. 敏感性分析：可以进行简单的敏感性分析来证明模型的稳健性。例如，随机剔除10%的样本后重新计算权重，看看权重的变化。如果挺稳定，责说明结论很可靠。如果用一小段话描述敏感性分析的结果，就会很亮眼。

参考资料

【大师兄数学建模】第4讲 熵权法_哔哩哔哩_bilibili

史聪聪. (2022). 基于熵权法和数据包络分析的高校信息化治理效能评价研究 [硕士学位论文, 安徽建筑大学].

2021年国赛C题优秀论文. (2021). 生产企业原材料订购与运输的评价与规划模型.

Zhu, Y., Tian, D., & Yan, F. (2020). Effectiveness of Entropy Weight Method in Decision-Making. Mathematical Problems in Engineering, 2020, 1-5.

Zardari, N. H., Ahmed, K., Shirazi, S. M., & Yusop, Z. B. (2014). Weighting Methods and their Effects on Multi-Criteria Decision Making Model Outcomes in Water Resources Management. Springer.