【数模学习笔记】模糊综合评价(FCE)的原理和过程详解
前言和简述
这个模型是用来解决什么问题的?
对受到多个模糊性因素影响的对象进行综合评价。用来解决现实世界的评价问题,因为许多评价标准并非“非黑即白”,而是有一定的的模糊性。(一个人有多少根头发才算“秃子”?)
主要应用于两大类评价场景,其具体功能由评语集 V的构建方式决定:
- 分类问题:当评语集是一组预设的等级,如
V = {优秀, 良好, 一般, 较差} - 排序问题:当评语集是多个待选方案,如
V = {方案一, 方案二, 方案三}时
为什么需要学习这个模型?它在数学建模中的地位或常用性如何?
应用领域很广泛,涵盖大部分需要进行综合评价的场景;模型生态强大,经常与其他模型结合,形成更强大的评价体系。最经典的组合:层次分析法 + 模糊综合评价。
- 评价一个产品的舒适度
- 评价一个方案的风险水平
- 评价一个景区的景色优美程度
过程
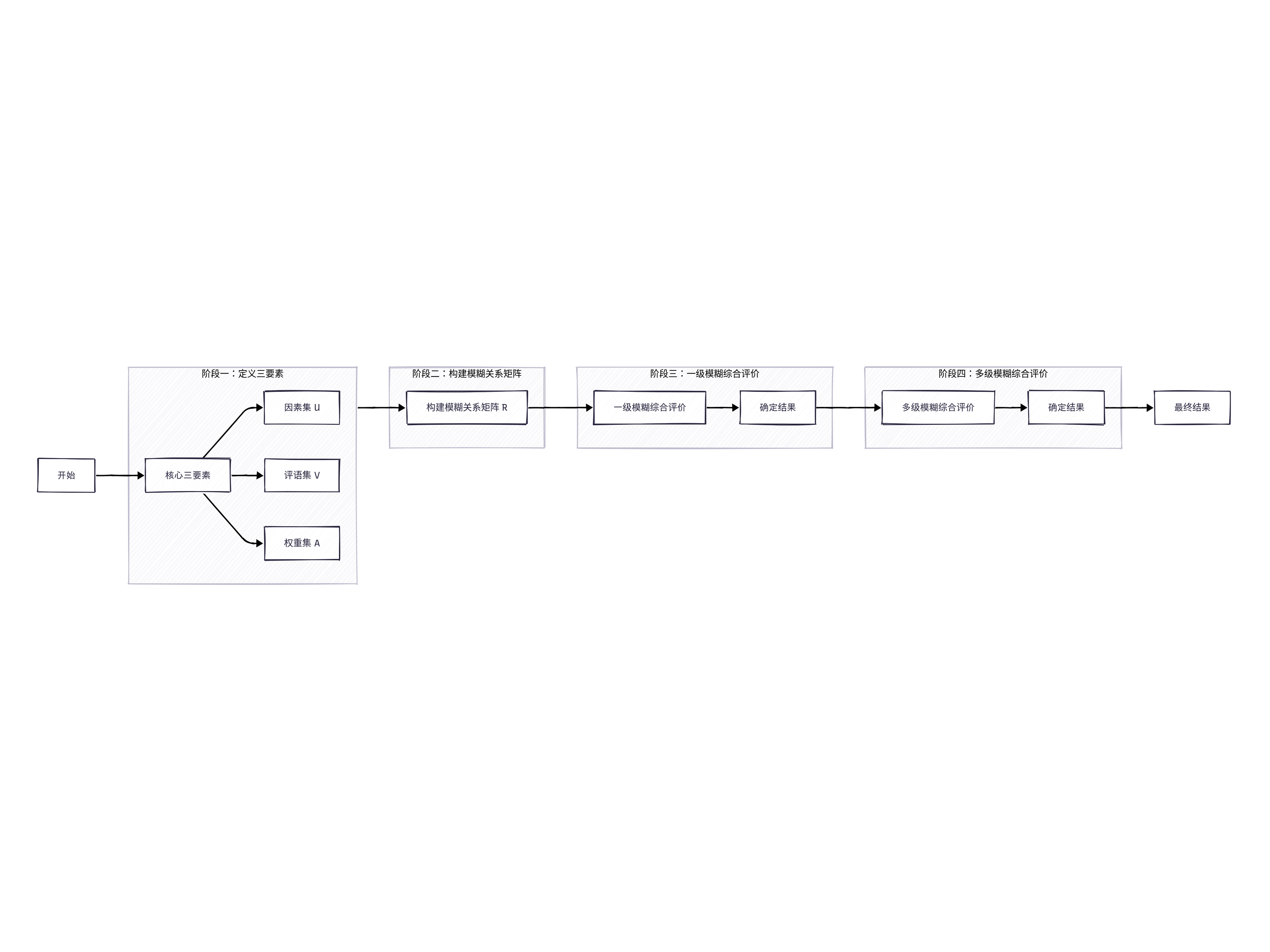
整体思路如下图所示:
graph TD
A[开始] --> B[核心三要素]
subgraph "阶段一:定义三要素"
B1[因素集 U]
B2[评语集 V]
B3[权重集 A]
B --> B1
B --> B2
B --> B3
end
B3 --> C
subgraph "阶段二:构建模糊关系矩阵"
C[构建模糊关系矩阵 R]
C1[隶属度确定方法]
C1a[模糊统计法]
C1b[隶属函数法]
C .-> C1 --> C1a
C1 --> C1b
end
C --> D[一级模糊综合评价]
%% 添加一个不可见的链接,强制 D 节点在 C1b 节点的下方
C1b ~~~ D
subgraph "阶段三:一级模糊综合评价"
D1[计算 B = A × R]
D2[最大隶属度原则确定结果]
D --> D1 --> D2
end
D2 --> E[多级模糊综合评价(如有层级)]
subgraph "阶段四:多级模糊综合评价"
E1[划分多级因素集]
E2[每一级分别计算 B_i]
E3[将 B_i 汇聚成 R_level1]
E4[最终综合评价 B_final = A × R_level1]
E5[最大隶属度原则确定最终结果]
E --> E1 --> E2 --> E3 --> E4 --> E5
end
E5 --> F[最终输出评价结果]
1. 核心三要素:因素集、评语集、权重集
构建模糊综合评价模型的第一步是明确定义三个核心集合 。
- 因素集 U:指评价所涉及的所有指标或标准的集合。它是评价体系的基石,决定了从哪些维度去衡量评价对象。其数学表示为:
其中 $n$ 是评价指标的总数。
- 评语集 V:指对评价对象可能做出的所有评价结果的集合。如前所述,这个集合的定义决定了模型的最终目的是分类还是排序。其数学表示为:
其中 $m$ 是评价等级或备选方案的总数。
- 权重集 A:一个模糊向量,表示因素集中各个指标 $u_i$ 的相对重要程度。权重的分配对最终结果有直接且显著的影响。其数学表示为:
其中 $a_i$ 为第 $i$ 个因素的权重,且需满足非负性和归一性,即 $a_i \geq 0$ 且 $\sum_{i=1}^{n} a_i = 1$。
2. 构建模糊关系矩阵 R:确定隶属度
模糊关系矩阵 $R$ 是模型的核心,它定量地描述了每个评价指标与每个评语之间的模糊关系。它是一个 $n \times m$ 的矩阵,其中元素 $r_{ij}$ 表示第 $i$ 个因素 $u_i$ 对于第 $j$ 个评语 $v_j$ 的隶属度,即 $u_i$ 被评定为 $v_j$ 的可能性(当用于分类)或程度(当用于排序) 。
$$ R = \begin{bmatrix} r_{11} & r_{12} & \cdots & r_{1m} \\ r_{21} & r_{22} & \cdots & r_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ r_{n1} & r_{n2} & \cdots & r_{nm} \end{bmatrix} $$确定隶属度 $r_{ij}$ 主要有两种方法 :
-
模糊统计法:这是一种基于经验数据的客观方法。隶属度:先调查、打分,然后统计每个指标在各个评语等级上的得票频率。在员工考核中,若有50名同事对某员工的“工作态度”进行评价,其中有10人评为“优秀”,25人评为“良好”,则“工作态度”对“优秀”的隶属度为 $10/50=0.2$,对“良好”的隶属度为 $25/50=0.5$ 。
-
F分布确定隶属函数(重点):当评价指标是可以用具体数值衡量的连续变量时(如成本、温度、尺寸等),可以构建一个数学函数 $\mu(x)$,将具体的指标值映射到 $[0,1]$ 区间内的隶属度。根据指标特性的不同,隶属函数通常分为以下几类 :
-
极大型(越大越优型):适用于“利润”、“产量”等指标,其隶属度随指标值增大而增大。
-
极小型(越小越优型):适用于“成本”、“污染”等指标,其隶属度随指标值增大而减小。
-
中间型(区间最优型):适用于“温度”、“pH值”等指标,其隶属度在某个最佳区间内为1,向两侧逐渐减小。
常用的隶属函数有梯形分布、正态分布、柯西分布等(如下图)。选择和构建合适的隶属函数是此方法的关键,需要对问题有深刻的理解。
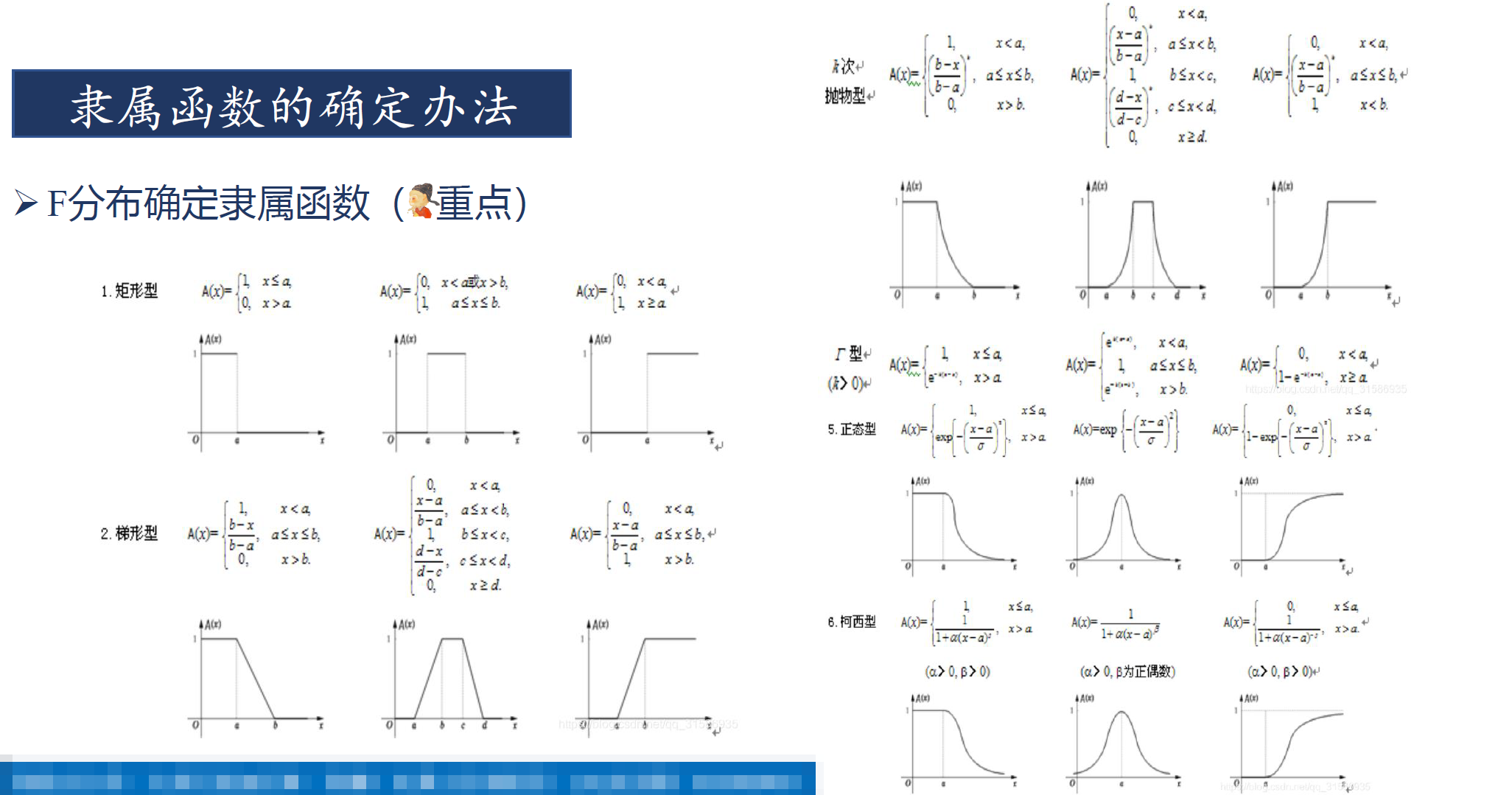
image-20250719223322974
-
3. 一级模糊综合评价
当评价指标不多且没有明显的层次结构时,采用一级模糊综合评价。
计算过程与结果解析
计算的核心是模糊变换,即通过权重集 $A$ 和模糊关系矩阵 $R$ 的复合运算,得到综合评价结果向量 $B$。
$$ B = A \circ R = (b_1, b_2, \dots, b_m) $$这里的复合算子“$\circ$”指的是是矩阵乘法。计算得到的向量 $B$ 中的每个元素 $b_j = \sum_{i=1}^{n} a_i \cdot r_{ij}$,代表了评价对象从总体上看,隶属于评语 $v_j$ 的综合隶属度。
最后根据最大隶属度原则,在 $B$ 中找到值最大的元素 $b_k$,则其对应的评语 $v_k$ 即为最终的综合评价结果 。
案例详解:员工绩效考核(分类问题,带有评价色彩的模糊综合评价)
以员工绩效考核为例,完整演示一级模糊综合评价的过程 。
-
确定三要素:
-
因素集 $U = {u_1(\text{政治表现}), u_2(\text{工作能力}), u_3(\text{工作态度}), u_4(\text{工作成绩})}$
-
评语集 $V = {v_1(\text{优秀}), v_2(\text{良好}), v_3(\text{一般}), v_4(\text{较差}), v_5(\text{差})}$
-
权重集 $A = [0.25, 0.2, 0.25, 0.3]$
关于权重,如果题目没有给出数据则用AHP(在论文里写上一句“根据专家意见”即可),如果给了数据则用熵权法的TOPSiS,也可以不确定权重
权重集$$A$$需满足$$\sum_{i=1}^{n} a_{i} = 1$$
-
-
构建模糊关系矩阵 $R$: 通过模糊统计法(如群众评议和领导打分),得到各单因素评价结果,构成 $R$ 矩阵。
-
进行模糊综合评判: $$ B = A \cdot R = [0.25, 0.2, 0.25, 0.3] \cdot \begin{bmatrix} 0.1 & 0.5 & 0.4 & 0 & 0 \ 0.2 & 0.5 & 0.2 & 0.1 & 0 \ 0.2 & 0.6 & 0.2 & 0 & 0 \ 0.3 & 0.5 & 0.2 & 0 & 0 \end{bmatrix} = [0.175, 0.53, 0.275, 0.02, 0] $$
-
结果解析: 评价结果向量 $B$ 中,第二个元素 $0.53$ 最大,对应评语 $v_2$(良好)。所以这个员工的综合评价结果为“良好”。
案例详解:边坡设计方案选择(排序问题,不带有评价色彩的模糊综合评价)
当评语集是待选方案时,模型用于排序。以某露天煤矿的边坡设计方案选择为例 。
-
确定三要素:
- 因素集 $U = {u_1(\text{可采矿量}), u_2(\text{基建投资}), u_3(\text{采矿成本}), u_4(\text{不稳定费用})}$
- 评语集 $V = {v_1(\text{方案1}), v_2(\text{方案2}), \dots, v_5(\text{方案5})}$
- 权重集 $A = [0.25, 0.2, 0.2, 0.1, 0.25]$(不唯一)
-
构建模糊关系矩阵 $R$: 矩阵的每一行代表一个评价指标,每一列代表一个方案。元素 $r_{ij}$ 是通过隶属函数计算出的第 $j$ 个方案在第 $i$ 个指标下的“满意度”。例如,对于“可采矿量”(极大型指标),可以用 $r_{1j} = x_j / x_{\max}$ 来计算;对于“基建投资”(极小型指标),可以用 $r_{2j} = 1 - x_j / x_{\max}$ 来计算。计算后得到 $R$ 矩阵:
- 进行模糊综合评判: 计算 $B = A \cdot R$,得到每个方案的综合得分向量。
- 结果解析: 结果向量 $B$ 中的每个元素代表对应方案的最终得分。得分越高,方案越优。这里方案1得分最高($0.7435$),所以是最佳方案。
4. 多级模糊综合评价
当评价指标数量很多,且指标之间存在自然的逻辑分组时,应采用多级模糊综合评价。这种方法分层处理,将一个复杂问题分解为若干个简单的子问题。
二级模糊综合评价过程
其计算过程是一个“自下而上”的汇集过程 :
-
划分因素集:将总因素集 $U$ 划分为 $k$ 个一级子因素集 $U_1, U_2, \dots, U_k$。每个一级子因素集 $U_i$ 又包含若干个二级子因素。
-
进行二级评价:对每个一级子因素集 $U_i$(例如“工作绩效”)单独进行一次一级模糊综合评价。
- 确定其下属的二级指标的权重向量 $A_i$。
- 构建二级指标相对于最终评语集 $V$ 的模糊关系矩阵 $R_i$。
- 计算得到该一级子因素集的综合评价向量 $B_i = A_i \cdot R_i$。这个 $B_i$ 向量,实际上就是一级指标 $U_i$ 对最终评语集 $V$ 的综合隶属度。
-
进行一级评价:将二级评价的结果作为一级评价的输入。
- 将上一步计算出的所有 $B_i$ 向量作为行,构成一个新的、用于一级评价的模糊关系矩阵 $R_{\text{level1}}$。
- 使用一级指标的权重向量 $A$ 和这个新矩阵 $R_{\text{level1}}$,进行最终的模糊综合评价:$B_{\text{final}} = A \cdot R_{\text{level1}}$。
- 结果解析:根据最大隶属度原则,对 $B_{\text{final}}$ 进行解读。
案例详解:详细员工考核
以一个更复杂的员工考核为例,其指标体系包含4个一级指标和18个二级指标 。
-
因素集划分与权重:
- 一级因素:$U = {U_1(\text{工作绩效}), U_2(\text{工作态度}), U_3(\text{工作能力}), U_4(\text{学习特长})}$
- 一级权重:$A = [0.4, 0.3, 0.2, 0.1]$
- 二级因素及权重:每个一级因素下有多个二级因素及其对应权重,例如 $U_1$ 下有“工作量”、“工作效率”等,权重为 $A_1 = [0.2, 0.3, 0.3, 0.2]$。
-
二级评价计算: 假设已通过打分得到每个二级指标对评语集 $V = {\text{优秀, 良好, 一般, 较差, 差}}$ 的隶属度矩阵 $R_1, R_2, R_3, R_4$。
- 对“工作绩效”进行评价:$B_1 = A_1 \cdot R_1 = [0.39, 0.39, 0.26, 0.04, 0.01]$
- 对“工作态度”进行评价:$B_2 = A_2 \cdot R_2 = [0.25, 0.33, 0.235, 0.125, 0.06]$
- 对“工作能力”进行评价:$B_3 = A_3 \cdot R_3 = [0.15, 0.32, 0.355, 0.115, 0.06]$
- 对“学习特长”进行评价:$B_4 = A_4 \cdot R_4 = [0.27, 0.35, 0.26, 0.1, 0.02]$
-
一级评价计算: 将 $B_1, B_2, B_3, B_4$ 组合成一级评价的关系矩阵 $R_{\text{level1}}$。
进行最终计算:
$$ B_{\text{final}} = A \cdot R_{\text{level1}} = [0.4, 0.3, 0.2, 0.1] \cdot R_{\text{level1}} = [0.288, 0.354, 0.2355, 0.0865, 0.036] $$- 结果解析: 最终评价向量中,$0.354$ 为最大值,对应“良好”,故该员工的最终评价为“良好”。
三级及以上的模糊综合评价模型,其逻辑与二级模型完全相同,只是将“自下而上”的汇集过程再增加若干层次。
模型的优缺点:
优点
- 系统性、结构化:将复杂的评价问题分解为因素集、评语集、权重集等结构化元素,逻辑清晰,步骤明确 。
- 量化定性信息:其最核心的优势在于为那些模糊的(定性的、主观的)评价标准能够被量化 。
- 信息完整性高:模型在计算中考虑了每一个因素对每一个评语等级的贡献,相比简单的加权求和,能提供更全面的评价。
- 层次灵活性强:可以根据问题的实际复杂程度,灵活地构建为一级或多级结构,适用性强 。
缺点
- 双重主观性:模型的可靠性高度依赖于输入数据的质量。权重集A的确定(如使用AHP)依赖主观判断;模糊关系矩阵R的构建(特别是使用专家打分时)也很主观。可谓“Garbage in, garbage out”的风险被放大了 。
- 可能导致信息损失:最终决策时广泛采用的“最大隶属度原则”虽然简单,但可能隐藏重要信息。例如,两个方案的评价结果向量可能分别是$B_1 = [0.4, 0.41, 0.19]$和$B_2 = [0.1, 0.41, 0.49]$。第一个和第二个差别很大,直接取最大值会忽略这种分布上的差异,造成决策信息的损失。
- 计算量较大:当指标和评语等级数量增多时,需要确定的隶属度数量(n×m)会急剧增加,尤其是在多级模型中,工作量会变得非常庞大 。
我的思考与总结:
学习模糊综合评价,核心在于理解其如何用数学工具为“模糊”的概念的量化。
难点与克服:
-
隶属函数的确定:这是构建模型中最具挑战性的一步。
-
如果项目中有条件进行问卷调查或有历史数据(可以查找相关论文),应优先采用模糊统计法,更具客观性。
-
若无数据,则需选择标准隶属函数(如梯形、高斯等)。
选择标准隶属函数的话,关键在于充分论证所选函数形式与题目指标的匹配度,并在论文中清晰说明函数参数的确定依据。
-
-
权重的确定:这是另一个关键的主观输入环节。一个非常实用的策略是:“有数据用熵权,没数据用层次” 。当有客观的评价数据时,熵权法能根据数据本身的信息量来确定权重,客观性强;当缺乏数据,只能依赖专家经验时,就事用AHP。
与其他模型的联系或区别
- FCE vs. AHP:两者都善于处理多准则决策问题,且都采用了分层思想来分解复杂问题。根本区别在于评价的实现方式:AHP在各层级都依赖于“两两比较”来确定相对重要性,这种方式直观但可能逻辑不一致;而FCE在底层通过隶属度来描述绝对的归属关系,在有数据支持时可以更客观,但隶属函数的定义本身是一大难点。
- FCE vs. TOPSIS:两者都可以用于方案排序。FCE的排序依据是方案对一个模糊概念的隶属度得分;而TOPSIS的排序依据是各方案与“正理想解”和“负理想解”的几何距离。它们从不同哲学角度定义了“最优”,互补。
建模注意事项与小妙招
-
超越最大隶属度原则:为了避免信息损失,在报告结果时不应只提及最大隶属度对应的评语。更优的做法是将最终的评价向量B用柱状图进行可视化,完整展示在所有评语上的隶属度分布。如果评语集可以被量化(例如,优秀=5, 良好=4,...),可以计算一个最终的加权得分($$Score=\sum{bj⋅vj}$$),更精确的单一数值。
-
理由是关键:鉴于模型的高度主观性,论文中必须对每一个关键选择进行详尽的论证,包括:为什么选择这些因素(U),为什么设定这些评语(V),权重(A)是如何得出的,以及隶属度(R)的计算方法和参数选择依据。言之有理既可。
-
善用图表:对于多级模型,其层次结构会比较复杂。最好在论文中多使用层次结构图、表格和结果可视化图表,提高说服力 。
注意:在论文中“根据隶属度确定相关评语”的部分,最好画成直方图,方便审稿人阅读。
-
模糊综合评价的原理并不难,真正拉开差距的点在于模型的选取是否合理(例如因素集的选取)。另外,对于这种“没啥技术含量”的模型可以用图文并茂的方法充实文章。
参考资料
【大师兄数学建模】第3讲 模糊综合评价_哔哩哔哩_bilibili